[의학통계방법론] Ch19. Simple Linear Correlation

19 May 2022 in Study log / Study / 의학통계방법론 on R, Sas, Blog, Jekyll, Jupyter, Data, Python

Simple Linear Correlation
R 프로그램 결과
- 19장
SAS 프로그램 결과
- 19장

Simple Linear Correlation

예제 데이터 링크 바로가기

R 프로그램 결과

R 접기/펼치기 버튼

패키지

설치된 패키지 접기/펼치기 버튼

getwd()

## [1] "C:/Biostat"

library("foreign")
library("dplyr")
library("kableExtra")
library("GGally")
library("DescTools")
library("confintr")
library("diffcor")
library("remotes")
library("cower")
library("gtools")
library("psych")
library("ltm")
library("irr")

19장

19장 연습문제 불러오기

ex19_1a <- read.spss('Exam 19.1A.sav', to.data.frame=T)
ex19_12 <- read.spss('Exam 19.12.sav', to.data.frame=T)
ex19_13 <- read.spss('Exam 19.13.sav', to.data.frame=T)
ex19_14 <- read.spss('Exam 19.14.sav', to.data.frame=T)
ex19_15 <- read.spss('Exam 19.15.sav', to.data.frame=T)
ex19_16 <- read.spss('Exam 19.16.sav', to.data.frame=T)
ex19_17 <- read.spss('Exam 19.17.sav', to.data.frame=T)
ex19_18 <- read.spss('Exam 19.18.sav', to.data.frame=T)

EXAMPLE 19.1a

#데이터셋
ex19_1a %>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
WingLeingth	TailLength
10.4	7.4
10.8	7.6
11.1	7.9
10.2	7.2
10.3	7.4
10.2	7.1
10.7	7.4
10.5	7.2
10.8	7.8
11.2	7.7
10.6	7.8
11.4	8.3

해당 데이터는 새의 날개의 길이와 꼬리의 길이를 측정한 대한 데이터이다.
새의 날개의 길이와 꼬리의 길이에 대하여 상관계수와 결정계수를 구하여 보겠다.

wing<-ex19_1a$WingLeingth
tail<-ex19_1a$TailLength

n=nrow(ex19_1a) 
sum_X=sum(wing)
sum_X2=sum(wing^2)
sum_x2=sum((wing-mean(wing))^2) 

sum_Y=sum(tail)
sum_Y2=sum(tail^2)
sum_y2=sum((tail-mean(tail))^2)
sum_XY=sum(wing*tail)
sum_xy=sum((wing-mean(wing))*(tail-mean(tail)))
r=sum_xy/sqrt(sum_x2*sum_y2)
r2=r^2

cbind(n, sum_X, sum_X2, sum_x2, sum_Y, sum_Y2, sum_y2, sum_XY, sum_xy, r, r2) %>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
n	sum_X	sum_X2	sum_x2	sum_Y	sum_Y2	sum_y2	sum_XY	sum_xy	r	r2
12	128.2	1371.32	1.716667	90.8	688.4	1.346667	971.37	1.323333	0.8703546	0.7575171

Pearson의 상관계수는 정규성 가정에서 출발하지 않았으며, 정규분포를 따르지 않더라도 1차 선형적인 연관성이 강하다면 구할 수 있다.
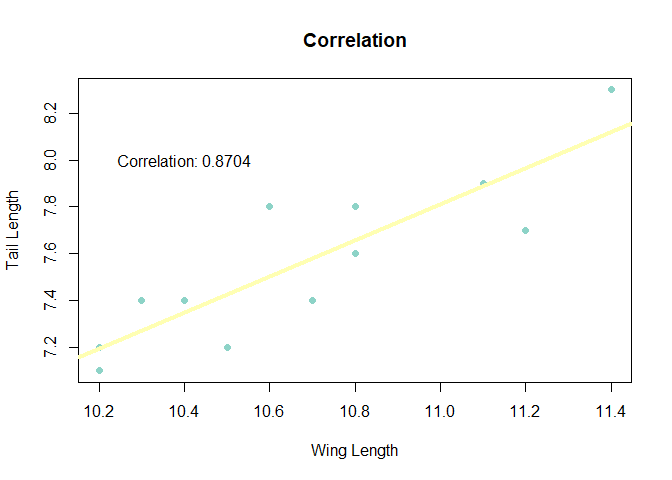
그래프를 그려서 선형성을 확인하여 보자.

plot(ex19_1a$WingLeingth,ex19_1a$TailLength,xlab = "Wing Length",ylab="Tail Length",main="Correlation",pch=19,col="#8dd3c7")
abline(lm(ex19_1a$TailLength ~ ex19_1a$WingLeingth), col = "#ffffb3", lwd = 4)
text(paste("Correlation:", round(r, 4)), x = 10.4, y = 8)

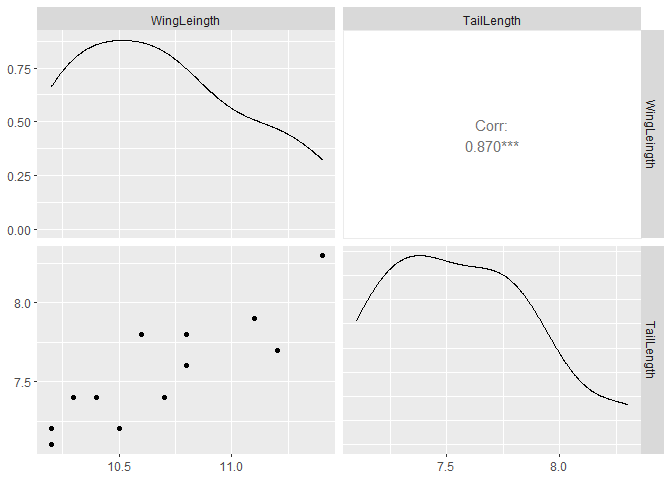
library("GGally")
ggpairs(ex19_1a, colums=1:2)

EXAMPLE 19.1b

상관계수에 대한 검정의 가설은 다음과 같다.

\[\begin{aligned} H_0 &: \rho=0 \\ H_A &: \rho \neq 0 \end{aligned}\]

R에 내장된 함수 cor.test()를 사용하여 양측검정을 시행하여 보겠다.

cor.test(ex19_1a$WingLeingth, ex19_1a$TailLength, alternative='two.sided')

## 
##  Pearson's product-moment correlation
## 
## data:  ex19_1a$WingLeingth and ex19_1a$TailLength
## t = 5.5893, df = 10, p-value = 0.0002311
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.5923111 0.9631599
## sample estimates:
##       cor 
## 0.8703546

먼저 기본 옵션으로 제공되는 t-test에 대한 결과를 보면, t-값=5.5893이고, p-value=0.0002311로 유의수준 5%하에 대립가설을 채택한다.
따라서 상관계수는 0이 아니다라고 말할 수 있다.
p-value=0.002311이 나왔는데 문제에서는 p-value=0.00012로 다른 것을 볼 수 있다.
예제에서는 표본상관계수가 이미 양수로 나왔기 때문에 우측만 보고 의사결정을 한 경우이다.
그렇다면 단측검정을 시행하여서 p-value가 같은지 확인하여 보겠다.

cor.test(ex19_1a$WingLeingth, ex19_1a$TailLength, alternative='greater')

## 
##  Pearson's product-moment correlation
## 
## data:  ex19_1a$WingLeingth and ex19_1a$TailLength
## t = 5.5893, df = 10, p-value = 0.0001156
## alternative hypothesis: true correlation is greater than 0
## 95 percent confidence interval:
##  0.6562825 1.0000000
## sample estimates:
##       cor 
## 0.8703546

p-value를 확인하여 보면 예제에서 나온 값이 같은 것을 볼 수 있다.
R에서 나오는 기본 함수로는 t-test로 진행하지만 F통계량으로도 가설검정을 진행할 수 있다.

f<-(1+abs(r))/(1-abs(r))
f

## [1] 14.42669

F 값은 14.4로써 3.72보다 크므로 귀무가설을 기각할 수 있다.

pf(f,10,10,lower.tail = F)

## [1] 0.000115553

단측가설의 대한 p-value=0.00012로써 유의수준 5%하에 귀무가설을 기각할 충분한 근거가 있으며,
예제에는 p-value는 양측에 대한 p-value가 구하여져 있기 때문에 좌측값 기준으로 계산된 p-value를 위에서 구한 p-value에 더해주면 양측에 대한 p-value가 구하여질 것이다.

EXAMPLE 19.2

이 예제에서는 상관계수가 0이 아닌 상수 0.750이 아닌지에 대한 검정을 하고자 한다.

\[\begin{aligned} H_0 &: \rho=0.750 \\ H_A &: \rho \neq 0.750 \end{aligned}\]

상관계수가 0이외에 다른 특정 값인지에 대해서도 검정을 진행하는 경우 tan변환을 통해 통계량을 구하고 검정을 진행한다.

\[\begin{aligned} z&=tanh^{-1}(r)=0.5\ ln(\frac{1+r}{1-r})\\ E(z)&=\zeta+\frac{\rho}{2(n-1)}\ \ \ Var(z)=\frac{1}{n-3}\ \ \ where,\ \zeta=tanh^{-1}(\rho) \end{aligned}\]

library("DescTools")
z<-FisherZ(r)
zeta<-FisherZ(0.75)
cat("z=",round(z,3),"zeta=",round(zeta,3))

## z= 1.335 zeta= 0.973

Fisherz 함수를 이용하여 상관계수와 검정할 0.75를 변환시켰으며, 이 두 값으로 통계량 Z값을 구하여 보자.

Z<-(z-zeta)/sqrt(1/(n-3)); Z

## [1] 1.084755

pnorm(Z,lower.tail = F)*2

## [1] 0.2780303

Z=1.08이고 이를 이용해 p-value를 구하면 0.28이다.
따라서 유의수준 0.05 하에서 귀무가설을 기각할 수 없고 모상관계수가 0.75가 아니라고 할만한 충분한 근거가 없다.
EXAMPLE 19.3

상관계수에 대해서도 신뢰한계를 구할 수 있다.

\[\begin{aligned} L_1=\frac{(1+F_\alpha)r+(1-F_\alpha)}{(1+F_\alpha)+(1-F_\alpha)r}=\frac{4.11-2.72}{4.72-2.37}=0.592\\ L_2=\frac{(1+F_\alpha)r-(1-F_\alpha)}{(1+F_\alpha)-(1-F_\alpha)r}=\frac{4.11+2.72}{4.72+2.37}=0.963 \end{aligned}\]

직접만든 함수로 구하여 보자.

f<-3.72
L1=((1+f)*r+(1-f))/((1+f)+(1-f)*r)
L2= ((1+f)*r-(1-f))/((1+f)-(1-f)*r)
cat("Confidence Limits for a Correlation Coefficient:",round(c(L1,L2),3))

## Confidence Limits for a Correlation Coefficient: 0.59 0.963

cor.test()를 사용하여 구하여 보자.

CI<-cor.test(ex19_1a$WingLeingth, ex19_1a$TailLength, alternative="two.sided", method="pearson")
CI$conf.int

## [1] 0.5923111 0.9631599
## attr(,"conf.level")
## [1] 0.95

ci_cor()를 사용하여 구하여 보자.

library("confintr")
ci_cor(ex19_1a$WingLeingth, ex19_1a$TailLength, method = "pearson",type="normal")

## 
##  Two-sided 95% normal confidence interval for the true Pearson
##  correlation coefficient
## 
## Sample estimate: 0.8703546 
## Confidence interval:
##      2.5%     97.5% 
## 0.5923111 0.9631599

EXAMPLE 19.4

이 예제는 상관계수가 0인지를 검정할 때 그 가설을 기각하기 위한 power를 구하는 예제이다.
pwr.r.test 패키지 함수를 이용하여 상관계수와 sample size, 유의수준, 양측검정인지 단측검정인지에 대해 입력하면 power를 계산할 수 있다.

library("pwr")
pw<-pwr.r.test(r, n=length(ex19_1a[,1]), sig.level = 0.05, alternative="two.sided")
cat("The power of the test is 1-β=",round(pw$power,2))

## The power of the test is 1-β= 0.98

EXAMPLE 19.5a

상관계수가 0인지를 검정할 때 그 가설을 기각하기 위한 sample size를 구하면 식은 다음과 같다.

\[n=(\frac{Z_{\beta(1)}+Z_\alpha}{\zeta_0})^2+3\]

pwr.r.test 패키지 함수를 이용하여 상관계수와 power, 유의수준, 양측검정인지 단측검정인지에 대해 입력하면 귀무가설을 기각할 수 있는 최소한의 sample size를 계산할 수 있다.

ex19_5a<-pwr.r.test(r=0.5, power=0.99, sig.level = 0.05, alternative = "two.sided")
cat("n=",round(ex19_5a$n,1))

## n= 63.1

계산 결과 n=63.1이므로 귀무가설을 기각하기 위한 최소한의 sample size는 64이다.

EXAMPLE 19.5b

pwr.r.test를 이용하는 방법 외에도 신뢰구간을 이용하여 귀무가설을 기각하기 위해 필요한 최소한의 sample size를 구할 수 있다.
예제 19.1a 에서 계산된 r이 0.87이고 모상관계수를 추정하기 위해 0.3보다 크지 않은 95% 신뢰구간이 필요한 경우 다음과 같은 프로세스를 사용할 수 있다.

#a)
e_195_b1<-function(n, alpha){
  v=n-2
  f_aa=round(qf(alpha/2, v, v, lower.tail = FALSE), 2)
  L1=round(((1+f_aa)*r+(1-f_aa))/((1+f_aa)+(1-f_aa)*r), 3)
  L2=round(((1+f_aa)*r-(1-f_aa))/((1+f_aa)-(1-f_aa)*r), 3)
  width_CI=L2-L1
  outcome=data.frame(f_aa, L1, L2, width_CI) %>% kbl(caption = "Ex 19.5 (b)") %>%  
    kable_classic(full_width = F, html_font = "Cambria")
  
  return(outcome)
}

e_195_b1(15, 0.05)

Ex 19.5 (b)
f_aa	L1	L2	width_CI
3.12	0.644	0.957	0.313

먼저 필요한 sample size를 15라고 가정하고 신뢰구간을 구한 결과 신뢰구간의 길이는 0.312이었고, 이는 0.3보다 조금 큰 수치이므로 sample size를 늘려보자.

e_195_b1(20, 0.05)

Ex 19.5 (b)
f_aa	L1	L2	width_CI
2.6	0.695	0.948	0.253

sample size를 20으로 가정하고 신뢰구간을 구한 결과 길이는 0.253이었고, 이는 0.3보다 작은 수치이므로 sample size를 줄여보자.

e_195_b1(16, 0.05)

Ex 19.5 (b)
f_aa	L1	L2	width_CI
2.98	0.658	0.955	0.297

이와 같이 계속해서 0.3에 가장 근사하는 sample size를 찾아나간 결과 귀무가설을 기각하기 위해 필요한 최소한의 sample size는 16이 나왔다.
다음은 r=0.87, z=1.3331로 고정된 경우 구하여 보자.

#b)
e_195_b2<-function(n, r, z){
  sigma_zz=sqrt(1/(n-3))
  z_crit=qnorm(0.025, lower.tail=FALSE)
  L1_F=z-z_crit*sigma_zz
  L2_F=z+z_crit*sigma_zz
  outcome=data.frame(z_crit, L1_F, L2_F) %>% kbl(caption = "Ex 19.5 (b)") %>%  
    kable_classic(full_width = F, html_font = "Cambria")
  
  return(outcome)
}

e_195_b2(15, 0.870, 1.3331)

Ex 19.5 (b)
z_crit	L1_F	L2_F
1.959964	0.7673071	1.898893

먼저 필요한 sample size를 15라고 가정하고 신뢰구간을 구한 결과 신뢰구간은 (0.7672,1.8990)이었고, 이를 다시 변환하면 (0.645,0.956)의 값이 나왔다.

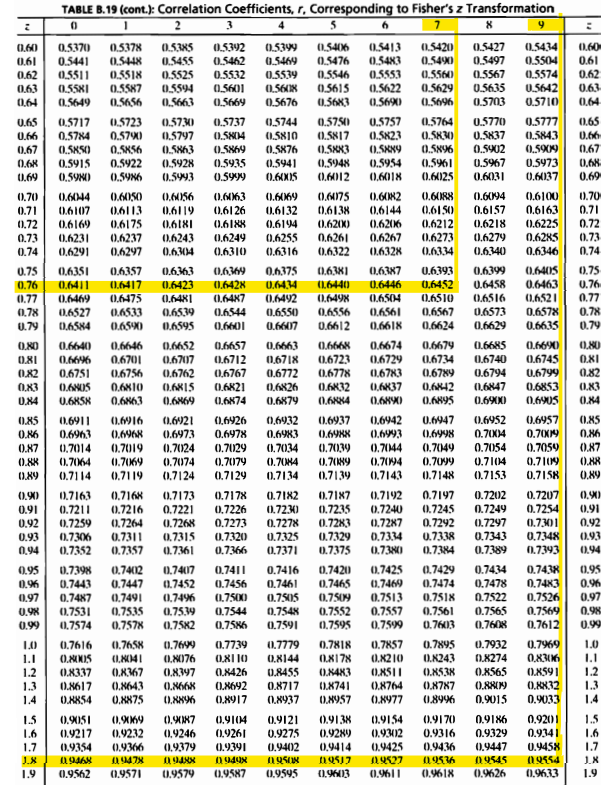
이 신뢰구간의 길이는 0.312이었고, 이는 0.3보다 조금 큰 수치이므로 sample size를 늘려보자.

e_195_b2(16, 0.870, 1.3331)

Ex 19.5 (b)
z_crit	L1_F	L2_F
1.959964	0.7895038	1.876696

sample size를 16라고 가정하고 신뢰구간을 구한 결과 신뢰구간은 (0.7894,1.8768)이었고, 이를 다시 변환하면 (0.658,0.954)의 값이 나왔다.

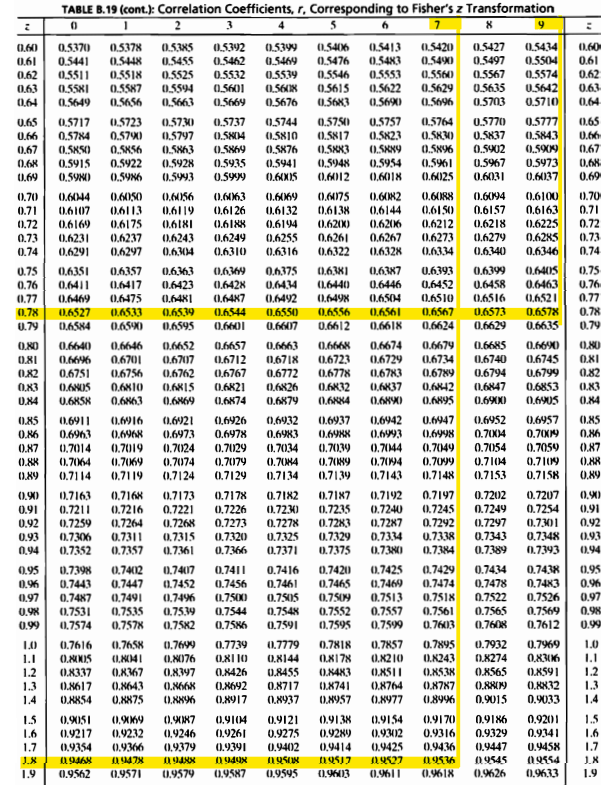
이 신뢰구간의 길이는 0.30이므로 sample size는 16으로 정한다.

EXAMPLE 19.6

이 예제에서는 독립인 서로 다른 두 집단의 모상관계수가 같은지에 대해 검정해보겠다.

\[\begin{aligned} H_0 &: \rho_1=\rho_2 \\ H_A &: \rho_1 \neq \rho_2 \end{aligned}\]

직접만든 함수로 구하여 보자.

r1= 0.78 ; r2=0.84
z1=1.0454 ; z2=1.2212
n1=98 ; n2=95
Z=(z1-z2)/sqrt((1/(n1-3))+(1/(n2-3)))
p<-round(pnorm(Z)*2,2)
cat("Z=",round(Z,3),"p-value=",round(p,2),"\nTherefore, do not reject H0.")

## Z= -1.202 p-value= 0.23 
## Therefore, do not reject H0.

diffcor.two()를 사용하여 구하여 보자.

library("diffcor")
diffcor.two(0.78, 0.84, 98, 95, alpha = 0.05, cor.names = NULL,alternative = "two.sided")

##     r1   r2   LL1   UL1   LL2   UL2      z     p Cohen_q
## 1 0.78 0.84 0.688 0.847 0.769 0.891 -1.202 0.229  -0.176

p-value는 모두 유의수준 0.05보다 크게 나타났고 귀무가설을 기각할 수 없다.
따라서 서로 다른 독립된 두 집단의 모상관계수가 다르다고 말할만한 충분한 근거가 없다.
귀무가설이 채택될 경우 공통상관계수를 구할 수 있으며 계산하면 공통상관계수는 0.81이다.

EXAMPLE 19.7

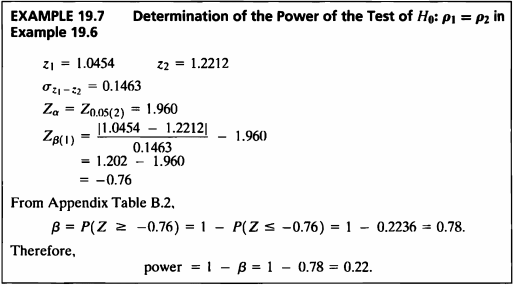
이 예제는 두 상관계수를 비교할 때의 검정력을 구하는 문제이다.

직접만든 함수로 구하여 보자.

z1=1.0454 ; z2=1.2212
sigma_12=0.1463
z_a=qnorm(0.025, lower.tail = FALSE)
z_b=round(((abs(z1-z2))/sigma_12)-z_a, 2)
beta=1-pnorm(z_b)
power.method2 = pnorm(z_b)
data.frame(power.method2) %>% kbl(caption = "Ex 19.7:방법1") %>%  
  kable_classic(full_width = F, html_font = "Cambria")

Ex 19.7:방법1
power.method2
0.2236273

power.indep.cor()를 사용하여 구하여 보자.

library("remotes")
# remotes::install_github('m-Py/cower')
# install_github("m-Py/cower")
library("cower")
e_197=power.indep.cor(r1=0.78, r2=0.84, n1=98, n2=95, sig.level = 0.05, alternative = "two.sided")
power.method1 = e_197$power
data.frame(power.method1) %>% kbl(caption = "Ex 19.7:방법2") %>%  
    kable_classic(full_width = F, html_font = "Cambria")

Ex 19.7:방법2
power.method1
0.2242004

검정통계량 값은 -0.76이고 이를 이용하여 정규분포표에서 값을 구하면 0.78이다. 따라서 검정력은 1-0.78=0.22가 된다.

EXAMPLE 19.8

이 예제는 두 상관계수를 비교할 때의 sample size를 구하는 문제이다.

z_alpha= round(qnorm(0.05/2, lower.tail = F), 4)
z_beta=round(qnorm(0.10,lower.tail = F), 4)
n_198=2*(((z_alpha+z_beta)/(0.5000))^2)+3
sample.size = ceiling(n_198)
cbind(z_alpha, z_beta, n_198, sample.size) %>% kbl(caption = "Ex 19.8") %>%  
  kable_classic(full_width = F, html_font = "Cambria")

Ex 19.8
z_alpha	z_beta	n_198	sample.size
1.96	1.2816	87.06376	88

두 값들의 차이를 이용하여 sample size를 구했고, 그 결과 상관계수 간 0.5의 차이를 발견하기 위해 귀무가설을 기각하기 위한 최소의 필요한 sample size는 88이다.

EXAMPLE 19.9

이 예제는 세 개의 상관계수를 비교하는 문제이다.

\[\begin{aligned} H_0 &: \rho_1=\rho_2=\rho_3\\ H_A &: All \ three \ population \ correlation \ coefficients \ are \ not \ equal. \end{aligned}\]

n=c(24,29,32)
r=c(0.52, 0.56, 0.87)

test.three_sample_corr <- function(n,r) {
  z = round(0.5*log((1+r)/(1-r)), 4)
  z_square = round(z^2, 4)
  n_minus_3 = n-3
  n_3_z = n_minus_3*z
  n_3_z_sqaure = n_minus_3*z_square
  test.stat = round(sum(n_3_z_sqaure) - (sum(n_3_z)^2)/sum(n_minus_3), 3)
  df = length(n)-1
  p.value = round(1 - pchisq(test.stat, df), 4)
  result.df = data.frame(test.stat, df, p.value)
  result.df<-result.df %>% kbl(caption = "Ex 19.9") %>%  
    kable_classic(full_width = F, html_font = "Cambria")
  return(result.df)
}

test.three_sample_corr(n,r)

Ex 19.9
test.stat	df	p.value
9.478	2	0.0087

검정통계량 값은 9.478이고 p-value는 0.0087로 유의수준 하에서 귀무가설을 기각하게 된다.
따라서 적어도 하나 이상의 상관계수는 같지 않다고 할 수 있다.
귀무가설이 기각되지 않았다면, common correlation coefficient를 계산하는 것이 적절했을 것이다.

common.corr <- function(n,r) {
  z = round(0.5*log((1+r)/(1-r)), 4)
  z_square = round(z^2, 4)
  n_minus_3 = n-3
  n_3_z = n_minus_3*z
  n_3_z_sqaure = n_minus_3*z_square
  z.w = sum(n_3_z)/sum(n_minus_3)
  r.w = round((exp(2*z.w)-1) / (exp(2*z.w)+1), 4)
  r.w <- data.frame(r.w)
  r.w <- r.w %>% kbl(caption = "Ex 19.9") %>%  
    kable_classic(full_width = F, html_font = "Cambria")
  
  return(r.w)
}
common.corr(n,r)

Ex 19.9
r.w
0.7086

common correlation coefficient는 0.7086으로 계산되었다.

EXAMPLE 19.10

상관계수 변환 시 z-변환이 편향되는 점으로 편향 극복을 위해 수정된 검정통계량 값을 계산하여야 한다.
Example 19.9와 동일한 가설을 correction for bias를 이용해 다시 구하여 보겠다.

n=c(24,29,32)
r=c(0.52, 0.56, 0.87)

test.corr_correction <- function(n,r) {
  z = round(0.5*log((1+r)/(1-r)), 4)
  z_square = round(z^2, 4)
  n_minus_3 = n-3
  n_3_z = n_minus_3*z
  n_3_z_sqaure = n_minus_3*z_square
  z.w = sum(n_3_z)/sum(n_minus_3)
  r.w = round((exp(2*z.w)-1) / (exp(2*z.w)+1), 2)

  test.stat = round(sum(n*t((r- r.w)^2) / (1 - r*r.w)^2), 4)
  df = length(n)-1
  p.value = round(1 - pchisq(test.stat, df), 4)
  result.df = data.frame(test.stat, p.value)
  result.df<-result.df %>% kbl(caption = "Ex 19.10") %>%  
    kable_classic(full_width = F, html_font = "Cambria")
  return(result.df)
}

test.corr_correction(n,r)

Ex 19.10
test.stat	p.value
9.5805	0.0083

계산된 검정통계량은 9.5805, p-value는 0.0083으로 유의수준 0.05보다 작았다.
즉, 유의수준 5%하에 세 개의 모집단 상관 계수가 모두 같지 않다고 말할 충분한 증거가 있다.
이는 Example 19.9의 가설검정 결과와 동일하다.

EXAMPLE 19.11

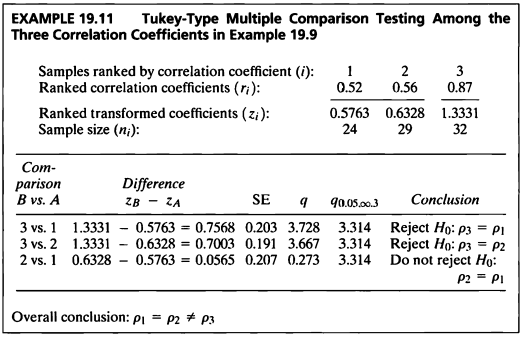
이 예제에서는 앞선 상관계수 검정을 통해 각 상관계수들이 모두 같지 않음을 확인했으므로 다중비교를 진행한다.
Z-변환을 이용하여 Tukey의 다중비교를 진행하였다.

library("gtools")
z = round(0.5*log((1+r)/(1-r)), 4)
comb<-combinations(3, 2, v = 1:3)

comb <- data.frame(comb)
comb<-comb[order(comb$X2, decreasing = T),]

ex19.11_result = vector()
for (k in 1:3) {
  compar_vec = vector()
  i=comb[k,2]
  j=comb[k,1]
  
  compar=paste0(i," vs. ",j)
  compar_vec = c(compar_vec, "Comparison"=compar)
  
  diff= z[i]-z[j]
  compar_vec = c(compar_vec, "Difference"=diff)
  
  SE = round(sqrt(1/2*(1/(n[i]-3) + 1/(n[j]-3))), 3)
  compar_vec = c(compar_vec, "SE"=SE)
  
  q = round((z[i]-z[j]) / round(sqrt(1/2*(1/(n[i]-3) + 1/(n[j]-3))), 3), 3)
  compar_vec = c(compar_vec, "q"=q)
  compar_vec = c(compar_vec, "critical.value"=3.314)
  
  if (q > 3.314) {
    compar_vec = c(compar_vec, "Conclusion"="Reject H0")
  }
  else {
    compar_vec = c(compar_vec, "Conclusion"="Do not reject H0")
  }
  ex19.11_result<- rbind(ex19.11_result, compar_vec)
}

rownames(ex19.11_result) <- c(rep(" ", 3))

ex19.11_result %>% kbl(caption = "Ex 19.11") %>%  
  kable_classic(full_width = F, html_font = "Cambria")

Ex 19.11
Comparison	Difference	SE	q	critical.value	Conclusion
3 vs. 1	0.7568	0.203	3.728	3.314	Reject H0
3 vs. 2	0.7003	0.191	3.666	3.314	Reject H0
2 vs. 1	0.0565	0.207	0.273	3.314	Do not reject H0

각각의 q 통계량을 3.314와 비교하면 그룹 3과 그룹1,2는 상관계수가 같다는 귀무가설을 기각했지만, 그룹 1과 그룹2는 귀무가설을 기각하지 못했다.
따라서 그룹 1과 그룹 2의 상관계수는 같으나 그룹 3의 상관계수는 다르다고 할 수 있다.

EXAMPLE 19.12

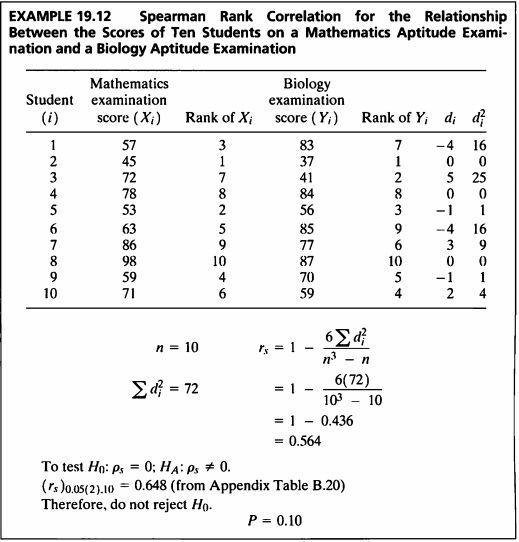
#데이터셋
ex19_12 %>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
Student	X	Y
1	57	83
2	45	37
3	72	41
4	78	84
5	53	56
6	63	85
7	86	77
8	98	87
9	59	70
10	71	59

n이 10 이상이고 순위상관계수가 0.9 이하이면 Fisher’s z-변환은 Spearman의 상관계수에도 사용될 수 있다.

ex19_12.result <-cor.test(ex19_12$X, ex19_12$Y, method="spearman")
ex19_12.result

## 
##  Spearman's rank correlation rho
## 
## data:  ex19_12$X and ex19_12$Y
## S = 72, p-value = 0.09579
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.5636364

ex19_12.result_table <- cbind("statistic"=ex19_12.result$statistic, "r"=round(ex19_12.result$estimate, 3),
      "p.value"=round(ex19_12.result$p.value, 3))
rownames(ex19_12.result_table)=c(" ")

ex19_12.result_table %>% kbl(caption = "Ex 19.12") %>%  
    kable_classic(full_width = F, html_font = "Cambria")

Ex 19.12
	statistic	r	p.value
	72	0.564	0.096

계산된 검정통계량 값은 0.564, p-value는 0.096으로 유의수준 0.05보다 크므로 귀무가설을 기각할 수 없다.
즉, 순위상관계수는 0이라고 말할 수 있으며, 수학시험 점수와 생물시험 점수 간 상관관계가 있다는 근거가 충분하지 않다고 말할 수 있다.

EXAMPLE 19.13

#데이터셋
ex19_13 %>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
Student	X	Y
1	10.4	7.4
2	10.8	7.6
3	11.1	7.9
4	10.2	7.2
5	10.3	7.4
6	10.2	7.1
7	10.7	7.4
8	10.5	7.2
9	10.8	7.8
10	11.2	7.7
11	10.6	7.8
12	11.4	8.3

이 예제에서는 Example 19.1 데이터를 가지고 특정 종의 새에 대한 날개와 꼬리 사이에 순위 상관성이 존재하는지 확인하기 위해 검정할 것이다.

\[\begin{aligned} H_0 &: \rho_s=0 \\ H_A &: \rho_s \neq 0 \end{aligned}\]

cor.test(ex19_13$X,ex19_13$Y,method = "spearman", exact = F)

## 
##  Spearman's rank correlation rho
## 
## data:  ex19_13$X and ex19_13$Y
## S = 42.59, p-value = 0.0004467
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.8510852

둘 사이에 순위 상관계수는 0.851이며 test 결과 p-value가 0.0004로 유의수준 0.05 보다 작기 때문에 귀무가설을 기각한다.
즉, 새의 날개와 꼬리 간에 순위 상관 관계가 존재한다고 할 수 있다.

EXAMPLE 19.14

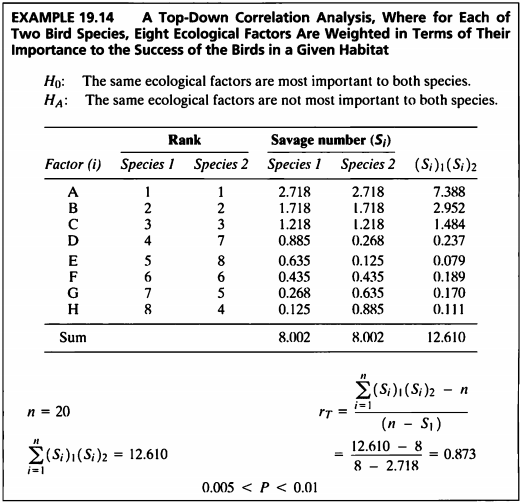
#데이터셋
ex19_14 %>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
Factor	Species1	Species2
A	1	1
B	2	2
C	3	3
D	4	7
E	5	8
F	6	6
G	7	5
H	8	4

\[\begin{aligned} H_0 &: The \ same \ ecological \ factors \ are \ most \ important \ to \ both \ species. \\ H_A &: The \ same \ ecological \ factors \ are \ not \ most \ important \ to \ both \ species. \end{aligned}\]

가중 순위 상관계수를 구하기 위해선 savage score을 사용한다.

j.inverse <- ex19_14$Species1^(-1)
savage.number1 = vector()
savage.number2 = vector()
for (k in 1:8) {
  S1 = round(sum(j.inverse[ex19_14$Species1[k]:8]), 3)
  savage.number1 = c(savage.number1, S1)
  
  S2 = round(sum(j.inverse[ex19_14$Species2[k]:8]), 3)
  savage.number2 = c(savage.number2, S2)
}

ex19_14.result <- cbind(ex19_14, savage.number1, savage.number2,
                        "(S1)(S2)"=round(savage.number1*savage.number2, 3))

ex19_14.result %>% kbl(caption = "Ex 19.14") %>%  
    kable_classic(full_width = F, html_font = "Cambria")

Ex 19.14
Factor	Species1	Species2	savage.number1	savage.number2	(S1)(S2)
A	1	1	2.718	2.718	7.388
B	2	2	1.718	1.718	2.952
C	3	3	1.218	1.218	1.484
D	4	7	0.885	0.268	0.237
E	5	8	0.635	0.125	0.079
F	6	6	0.435	0.435	0.189
G	7	5	0.268	0.635	0.170
H	8	4	0.125	0.885	0.111

summation = sum(round(savage.number1*savage.number2, 3))
n = length(ex19_14$Factor)
r.T = round((summation-n) / (n-savage.number1[1]), 3)
cbind(n, r.T) %>% kbl(caption = "Ex 19.14") %>%  
    kable_classic(full_width = F, html_font = "Cambria")

Ex 19.14
n	r.T
8	0.873

Top down correlation 분석 결과, 상관계수는 0.873으로 계산되었다.

cor.test(savage.number1,savage.number2)

## 
##  Pearson's product-moment correlation
## 
## data:  savage.number1 and savage.number2
## t = 4.3616, df = 6, p-value = 0.004762
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.4337146 0.9765680
## sample estimates:
##       cor 
## 0.8719087

검정 결과 상관계수는 0.8719087이며 이에 대한 검정 결과 p-value=0.004762 이므로 0.05보다 작기 때문에 동일한 생태적 요인이 두 종 모두에게 가장 중요한 것은 아니라는 결론을 내릴 수 있다.

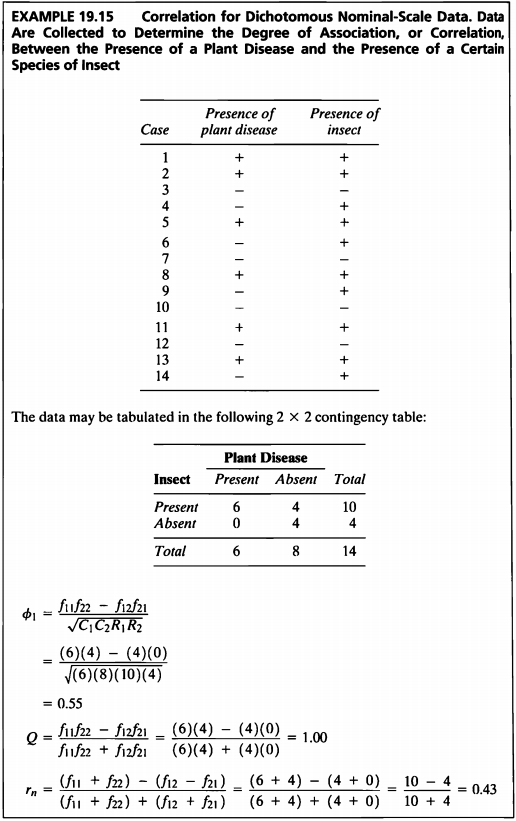
EXAMPLE 19.15

#데이터셋
ex19_15 %>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
Case	Disease	Insect
1	+	1
2	+	1
3	-	0
4	-	1
5	+	1
6	-	1
7	-	0
8	+	1
9	-	1
10	-	0
11	+	1
12	-	0
13	+	1
14	-	1

해당 데이터는 두 개의 이항형 변수, 특정 곤충의 유무와 식물 유병의 유무에 대하여 기록한 데이터이다.
phi 계수, Yule의 계수, 그리고 Ives and Gibbons의 계수로 상관관계를 알아보겠다.

library("psych")
cross.table<-table(ex19_15$Disease, ex19_15$Insect)

phi.coefficient <- phi(cross.table, digits = 2)
Yule.coefficient <- Yule(cross.table,Y=FALSE)
r.n = round(((cross.table[2,2] + cross.table[1,1]) - (cross.table[1,2] + cross.table[2,1])) / 
  ((cross.table[2,2] + cross.table[1,1]) + (cross.table[1,2] + cross.table[2,1])), 2)

ex19_15.result <- cbind(phi.coefficient, Yule.coefficient, r.n)

ex19_15.result %>% kbl(caption = "Ex 19.15") %>%  
    kable_classic(full_width = F, html_font = "Cambria")

Ex 19.15
phi.coefficient	Yule.coefficient	r.n
0.55	1	0.43

phi의 계수의 경우 0.55, Yule의 계수의 경우 0.97 (almost 1), 그리고 Ives and Gibbons의 계수의 경우 약 0.43의 값을 가진다.

EXAMPLE 19.16

#데이터셋
ex19_16 %>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
X	Y
0	8.8
0	8.4
0	7.9
0	8.7
0	9.1
0	9.6
1	9.9
1	9.0
1	11.1
1	9.6
1	8.7
1	10.4
1	9.5

예제 8.1은 변수 X가 약의 종류 2가지로 이항형이고, 변수 Y는 피가 응고되는 시간으로 연속형으로 하나의 변수가 이항형인 데이터이다.
Example 8.1 데이터를 사용하여 피가 응고되는 시간과 약의 종류 간의 상관성을 알아보도록 하겠다.

\[\begin{aligned} H_0 &: \rho_pb=0 \ (There \ is \ no \ correlation \ between \ blood-clotting \ time \ and \ drug.)\\ H_A &: \rho_pb \neq 0 \ (There \ is \ correlation \ between \ blood-clotting \ time \ and \ drug.) \end{aligned}\]

library("ltm")
r.pb = round(biserial.cor(ex19_16$Y,ex19_16$X,level=2), 4)
r.pb_square = round(r.pb^2, 4)

ex19_16.result <- cor.test(ex19_16$Y,ex19_16$X)
ex19_16.result

## 
##  Pearson's product-moment correlation
## 
## data:  ex19_16$Y and ex19_16$X
## t = 2.4765, df = 11, p-value = 0.03076
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.07058429 0.86434926
## sample estimates:
##       cor 
## 0.5983011

ex19_16.resultdf <- cbind(r.pb, r.pb_square,
                          "statistic"=round(ex19_16.result$statistic, 3),
                          "p.value"=round(ex19_16.result$p.value, 3)
                          )
rownames(ex19_16.resultdf) = c(" ")
ex19_16.resultdf %>% kbl(caption = "Ex 19.16") %>%  
    kable_classic(full_width = F, html_font = "Cambria")

Ex 19.16
	r.pb	r.pb_square	statistic	p.value
	0.5983	0.358	2.476	0.031

계산된 Point-Biserial 상관계수는 0.5983이다.
그리고 검정통계량은 2.476이며, p-value는 0.031으로 유의수준 5%하에 귀무가설을 기각한다.
즉, 혈액 응고 시간과 약물 사이에는 상관관계가 존재한다는 충분한 증거가 있다.

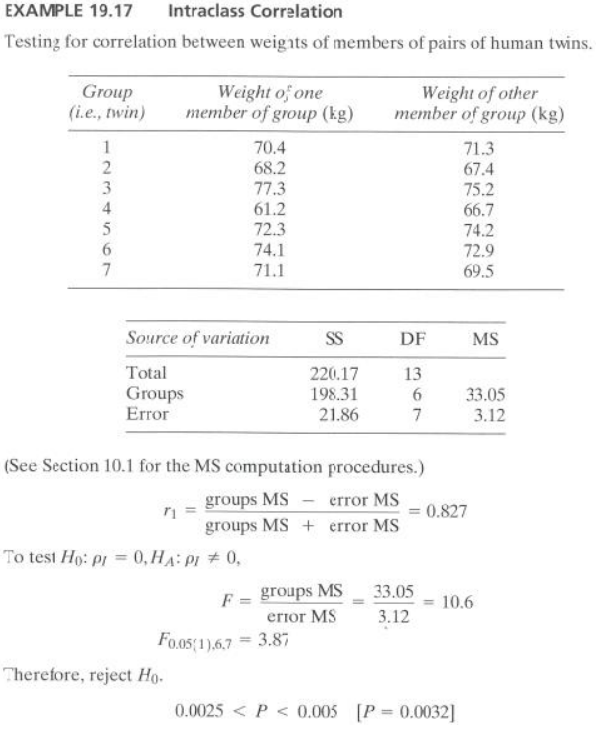
EXAMPLE 19.17

#데이터셋
ex19_17 %>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
Group	One	Other
1	70.4	71.3
2	68.2	67.4
3	77.3	75.2
4	61.2	66.7
5	72.3	74.2
6	74.1	72.9
7	71.1	69.5

해당 데이터는 쌍둥이들의 체중에 대해 기록한 데이터이다.
쌍둥이들의 체중 사이에 급내 상관계수에 대해 알아보고자 한다.
급내상관계수 과정에 대한 가정으로 이변량 정규 분포로 부터 랜덤하게 추출되어야 하며, 모집단의 분산이 동일해야 한다.

정규성 검정

shapiro.test(ex19_17$One)

## 
##  Shapiro-Wilk normality test
## 
## data:  ex19_17$One
## W = 0.94626, p-value = 0.6956

shapiro.test(ex19_17$Other)

## 
##  Shapiro-Wilk normality test
## 
## data:  ex19_17$Other
## W = 0.94088, p-value = 0.6466

정규성 검정결과, p-value가 각 그룹에서 0.6956, 0.6466으로, 두 그룹모두 정규성 가정을 만족하였다.

등분산성 검정

bartlett.test(ex19_17[,2:3])

## 
##  Bartlett test of homogeneity of variances
## 
## data:  ex19_17[, 2:3]
## Bartlett's K-squared = 0.99636, df = 1, p-value = 0.3182

분산 검정결과 p-value가 0.3182으로 유의수준 0.05보다 컸다. 그러므로 등분산 가정도 만족하였다.

library("irr")
ex19_17.result <- icc(ex19_17[,2:3], unit="single",r0=0)
ex19_17.resultdf<-cbind("r1"=round(ex19_17.result$value, 3),
                        "F.value"=round(ex19_17.result$Fvalue, 1),
                        "p.value"=round(ex19_17.result$p.value, 4))
ex19_17.resultdf %>% kbl(caption = "Ex 19.17") %>%  
    kable_classic(full_width = F, html_font = "Cambria")

Ex 19.17
r1	F.value	p.value
0.827	10.6	0.0033

일곱 쌍둥이 간 체중의 급내 상관관수는 0.827이며,
급내 상관관계를 확인하기 위한 검정 결과 F값=10.6, p-value= 0.00325로 유의수준 5%하에 귀무가설을 기각한다.
즉, 일곱 쌍둥이 간 체중에 대해 급내 상관관계가 있다고 할 수 있다.

EXAMPLE 19.18

#데이터셋
ex19_18 %>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
Group	A	B
1	0.22	0.21
2	0.26	0.23
3	0.30	0.27
4	0.33	0.27
5	0.36	0.31
6	0.39	0.33
7	0.41	0.37
8	0.44	0.38
9	0.47	0.40
10	0.51	0.43
11	0.55	0.47

해당 데이터는 두 개의 다른 원자 흡수 분광 광도계를 사용하여 뇌 조직의 납 농도 분석한 데이터이다.
이 예제의 데이터를 사용하여 일치 상관계수를 구해보도록 한다.
일치 상관계수는 데이턴의 일치도 혹은 재현성을 평가하기 위한 지표이다.

n<-length(ex19_18$A)
mean.A <- round(mean(ex19_18$A),3)
mean.B <- round(mean(ex19_18$B),3)
sum.A <- sum(ex19_18$A)
sum.B <- sum(ex19_18$B)
sum.AB <- sum(ex19_18$A*ex19_18$B)
sum.A2 <- sum(ex19_18$A^2)
sum.B2 <- sum(ex19_18$B^2)

ssA <- round(sum((ex19_18$A-mean.A)^2),5)
ssB <- round(sum((ex19_18$B-mean.B)^2),5)
ssAB <- sum((ex19_18$A-mean.A)*(ex19_18$B-mean.B))
r.c <- (2*ssAB) / (ssA+ssB+n*(mean.A-mean.B)^2)
r2.c <- r.c^2
r0 = ssAB / sqrt(ssA*ssB)
r02 = r0^2
U = (sqrt(n)*((mean.A-mean.B)^2)) / sqrt(ssA*ssB)

cbind(r.c, r2.c, r0, U) %>% kbl(caption ="Ex 19.18") %>%  
  kable_classic(full_width = F, html_font = "Cambria")

Ex 19.18
r.c	r2.c	r0	U
0.8373719	0.7011917	0.9937578	0.0991292

CCC(ex19_18$A, ex19_18$B, ci="z-transform", conf.level = 0.95)

## $rho.c
##         est    lwr.ci    upr.ci
## 1 0.8337058 0.6470369 0.9260831
## 
## $s.shift
## [1] 0.809665
## 
## $l.shift
## [1] -0.5826083
## 
## $C.b
## [1] 0.8388642
## 
## $blalt
##     mean delta
## 1  0.215  0.01
## 2  0.245  0.03
## 3  0.285  0.03
## 4  0.300  0.06
## 5  0.335  0.05
## 6  0.360  0.06
## 7  0.390  0.04
## 8  0.410  0.06
## 9  0.435  0.07
## 10 0.470  0.08
## 11 0.510  0.08

일치 상관계수는 데이터의 일치도 또는 재현성을 평가하기 위한 계수로 -1에서 1사이의 값을 가지고 절대값이 Pearson 상관계수보다 클 수 없으며, Pearson 상관계수가 0일 경우 일치 상관계수 또한 0이 나온다.
변수 A와 B에 대한 상관계수는 0.99로 0이 아님을 확인할 수 있고, 둘의 일치 상관계수는 0.8337이다.

SAS 프로그램 결과

SAS 접기/펼치기 버튼

19장

LIBNAME ex 'C:\Biostat';
RUN;

/*19장 연습문제 불러오기*/
PROC IMPORT DBMS=sav
DATAFILE='C:\Biostat\Exam 19.1A.sav'
OUT=ex.ex19_1a REPLACE;
RUN;

%macro chap19(name=,no=);
%do i=12 %to &no.;
	PROC IMPORT DBMS=sav
		DATAFILE="C:\Biostat\Exam 19.&i."
		OUT=ex.&name.&i. REPLACE;
	RUN;
%end;
%mend;

%chap19(name=ex19_,no=18);

EXAMPLE 19.1

PROC CORR DATA=ex.ex19_1A PEARSON;
     VAR WingLeingth TailLength;
RUN;

SAS 출력

Concordance Correlation Coefficient

CORR 프로시저


2 개의 변수:	WingLeingth TailLength


단순 통계량
변수	N	평균	표준편차	합	최솟값	최댓값	레이블
WingLeingth	12	10.68333	0.39505	128.20000	10.20000	11.40000	WingLeingth
TailLength	12	7.56667	0.34989	90.80000	7.10000	8.30000	TailLength


피어슨 상관 계수, N = 12 H0: Rho=0 가정하에서 Prob > \|r\|
	WingLeingth	TailLength
WingLeingth WingLeingth	1.00000	0.87035 0.0002
TailLength TailLength	0.87035 0.0002	1.00000

EXAMPLE 19.2

PROC IML;
	r= 0.870;
	n = 12;
	z = 0.5 * log((1 + r) / (1 - r));
	a = 0.5 * log((1 + 0.750) / (1 - 0.750));
	cz = round((z - a) / (sqrt(1 / (n - 3))), .0001);
	p = round((1 - probnorm(cz)) * 2, .01);
	PRINT cz p;
RUN;

ods graphics off;ods exclude all;ods noresults;
PROC CORR DATA=ex.ex19_1A nosimple fisher(rho0=0.750 biasadj=no);
    VAR WingLeingth TailLength;
    ODS OUTPUT FisherPearsonCorr=fisher;
RUN;
ods graphics on;ods exclude none;ods results;

PROC PRINT DATA=fisher;
RUN;

SAS 출력

Concordance Correlation Coefficient

cz	p
1.0804	0.28

Concordance Correlation Coefficient


OBS	Var	WithVar	NObs	Corr	ZVal	Lcl	Ucl	Rho0	pValue
1	WingLeingth	TailLength	12	0.87035	1.33454	0.592311	0.963160	0.75000	0.3259

EXAMPLE 19.3

proc iml;
	reset nolong;
	r=0.870;f=3.72;
	L1=((1+f)*r+(1-f))/((1+f)+(1-f)*r);
	L2=((1+f)*r-(1-f))/((1+f)-(1-f)*r);
	print L1 L2;
run;

SAS 출력

Concordance Correlation Coefficient

L1	L2
0.5890551	0.96331

EXAMPLE 19.4

PROC POWER;
    ONECORR DIST=fisherz
    NULLCORR=0
    CORR=0.870
    NTOTAL=12
    POWER=.;
RUN;

SAS 출력

Concordance Correlation Coefficient

The POWER Procedure

Fisher's z Test for Pearson Correlation


Fixed Scenario Elements
Distribution	Fisher's z transformation of r
Method	Normal approximation
Null Correlation	0
Correlation	0.87
Total Sample Size	12
Number of Sides	2
Nominal Alpha	0.05
Number of Variables Partialled Out	0


Computed Power
Actual Alpha	Power
0.0491	0.987

EXAMPLE 19.5a

PROC POWER;
    ONECORR DIST=fisherz
    NULLCORR=0
    CORR=0.5
    NTOTAL=.
    POWER=0.99;
RUN;

SAS 출력

Concordance Correlation Coefficient

The POWER Procedure

Fisher's z Test for Pearson Correlation


Fixed Scenario Elements
Distribution	Fisher's z transformation of r
Method	Normal approximation
Null Correlation	0
Correlation	0.5
Nominal Power	0.99
Number of Sides	2
Nominal Alpha	0.05
Number of Variables Partialled Out	0


Computed N Total
Actual Alpha	Actual Power	N Total
0.05	0.990	63

EXAMPLE 19.5b

PROC IML;	
    RESET nolog;
	r=0.870;f=2.98;
	L1=((1+f)*r+(1-f))/((1+f)+(1-f)*r);
	L2=((1+f)*r-(1-f))/((1+f)-(1-f)*r);
	diff=L2-L1;
    PRINT L1 L2 diff;
RUN;
QUIT;

SAS 출력

Concordance Correlation Coefficient

L1	L2	diff
0.6567733	0.9544068	0.2976335

EXAMPLE 19.6

PROC IML;	
    RESET nolog;
	r1=0.78;r2=0.84;
	z1=1.0454;z2=1.2212;
	n1=98;n2=95;
	
	z=(z1-z2)/sqrt((1/(n1-3))+(1/(n2-3)));
	
	p_value=probnorm(z)*2;
	zw=((n1-3)*z1+(n2-3)*z2)/(n1-3+n2-3);
	rw=(exp(2*(zw))-1)/(exp(2*(zw))+1);
    PRINT z p_value zw rw;
RUN;
QUIT;

SAS 출력

Concordance Correlation Coefficient

z	p_value	zw	rw
-1.20186	0.2294179	1.1318898	0.8116651

EXAMPLE 19.7

PROC IML;	
    RESET nolog;
	r1=0.78;r2=0.84;
	z1=1.0454;z2=1.2212;
	n1=98;n2=95;
	
	z_beta=(abs(z1-z2))/sqrt((1/(n1-3))+(1/(n2-3)))-1.96;
	beta=1-probnorm(z_beta);
	power=1-beta;
    PRINT beta power;
RUN;
QUIT;

SAS 출력

Concordance Correlation Coefficient

beta	power
0.7758165	0.2241835

EXAMPLE 19.8

PROC IML;	
    RESET nolog;
	z1=-probit(0.05/2);z2=-probit(0.10);
	diff=0.5;
	n=2*(((z1+z2)/diff)**2)+3;
    PRINT n;
RUN;
QUIT;

SAS 출력

Concordance Correlation Coefficient


n
87.059384

EXAMPLE 19.9

PROC IML;	
    RESET nolog;
	n={24,29,32};
	r={0.52,0.56,0.87};
    z=0.5*log((1+r)/(1-r));

	z2=z#z;
	n_z2=(n-3)#z2;
	n_z=(n-3)#z;
	chi=sum(n_z2)-(sum((n_z))**2/sum(n-3));
	p=1-probchi(chi,2);

	zw=(sum((n_z))/sum(n-3));
	rw=(exp(2*(zw))-1)/(exp(2*(zw))+1);
    PRINT chi p zw rw;
RUN;
QUIT;

SAS 출력

Concordance Correlation Coefficient

chi	p	zw	rw
9.4764447	0.0087542	0.8844225	0.7086279

EXAMPLE 19.10

PROC IML; 
	n1 = 24 ;   n2 = 29;    n3 = 32;
	r1 = 0.52; r2 = 0.56;  r3 = 0.87;

	rw = 0.71 ; 

	xp1 = round((n1 * (r1 - rw) ** 2) / (1 - r1 * rw) ** 2, .0001) ; 
	xp2 = round((n2 * (r2 - rw) ** 2) / (1 - r2 * rw) ** 2, .0001) ; 
	xp3 = round((n3 * (r3 - rw) ** 2) / (1 - r3 * rw) ** 2, .0001) ; 

	xp = xp1 + xp2 + xp3 ;
	p = round(1- probchi(xp, 2), .0001);

	PRINT xp1 xp2 xp3 p ; 

RUN; 

SAS 출력

Concordance Correlation Coefficient

xp1	xp2	xp3	p
2.1774	1.7981	5.6051	0.0083

EXAMPLE 19.11

PROC IML;
	%macro ex19_11(x1,x2);
	n={24,29,32}; 
	r={0.52,0.56,0.87}; 
	z=0.5*log((1+r)/(1-r));
	diff=round(z[&x1]-z[&x2],0.0001);
	se=round(sqrt((1/2)*((1/(n[&x1]-3))+(1/(n[&x2]-3)))),0.001) ; 
	q=round(diff/se,0.001); 
		if q>=3.314 then conclusion='Reject H0' ; 
		else if q <3.314 then conclusion='Do not reject H0' ; 
	PRINT diff se q conclusion; 
%mend ; 
%ex19_11 (3,1) ; 
%ex19_11 (3,2) ; 
%ex19_11 (2,1) ; 
QUIT;

SAS 출력

Concordance Correlation Coefficient

diff	se	q	conclusion
0.7567	0.203	3.728	Reject H0

diff	se	q	conclusion
0.7002	0.191	3.666	Reject H0

diff	se	q	conclusion
0.0565	0.207	0.273	Do not reject H0

EXAMPLE 19.12

PROC CORR DATA= ex.ex19_12 spearman nosimple;
	VAR x y ;
RUN;

SAS 출력

Concordance Correlation Coefficient

CORR 프로시저


2 개의 변수:	X Y


스피어만 상관 계수, N = 10 H0: Rho=0 가정하에서 Prob > \|r\|
	X	Y
X X	1.00000	0.56364 0.0897
Y Y	0.56364 0.0897	1.00000

EXAMPLE 19.13

PROC CORR DATA= ex.ex19_13 spearman nosimple;
	VAR x y ;
RUN;

SAS 출력

Concordance Correlation Coefficient

CORR 프로시저


2 개의 변수:	X Y


스피어만 상관 계수, N = 12 H0: Rho=0 가정하에서 Prob > \|r\|
	X	Y
X X	1.00000	0.85109 0.0004
Y Y	0.85109 0.0004	1.00000

EXAMPLE 19.14

DATA ex19_14;
INPUT species1 species2 @@; 
   CARDS;
2.718 2.718
1.718 1.718 
1.218 1.218
0.885 0.268
0.635 0.125
0.435 0.435
0.268 0.635
0.125 0.885
;
RUN;

PROC CORR DATA= ex19_14 pearson nosimple;
	VAR species1 species2 ;
RUN;

SAS 출력

Concordance Correlation Coefficient

CORR 프로시저


2 개의 변수:	species1 species2


피어슨 상관 계수, N = 8 H0: Rho=0 가정하에서 Prob > \|r\|
	species1	species2
species1	1.00000	0.87191 0.0048
species2	0.87191 0.0048	1.00000

EXAMPLE 19.15

ods graphics off; ods exclude all; ods noresults;
PROC FREQ DATA = ex.ex19_15;
	TABLES Disease*Insect / norow nocol nopercent expected chisq out=table19_15;
	TEST gamma;
	ODS OUTPUT ChiSq=ChiSq Gamma=Gamma;
RUN;
ods graphics on; ods exclude none; ods results;

PROC PRINT DATA=ChiSq label;
    WHERE Statistic="파이 계수";
    VAR Statistic Value;
RUN;

PROC PRINT DATA=Gamma label;
    VAR Label1 cValue1;
RUN;

PROC IML;	
    RESET nolog;
	f11=6; f12=4;
	f21=0; f22=4;

	r_n=round(((f11+f22)-(f12+f21))/((f11+f22)+(f12+f21)), 0.01);

	PRINT r_n;
RUN;
QUIT;

SAS 출력

Concordance Correlation Coefficient


OBS	통계량	값
5	파이 계수	0.5477

Concordance Correlation Coefficient


OBS	Label1	cValue1
1	감마	1.0000
2	ASE	0.0000
3	95% 신뢰하한	1.0000
4	95% 신뢰상한	1.0000

Concordance Correlation Coefficient


r_n
0.43

EXAMPLE 19.16

%macro biserial(version, data= ,contin= ,binary= ,out=);

%if &version ne %then %put BISERIAL macro Version 2.2;

options nonotes;
* exclude observations with missing variables *;
data &out;
 set &data;
 where &contin>.;
 if &binary>.;
 run;

* compute the ranks for the continuous variable *;
proc rank data=&out out=&out ;
 var &contin;
 ranks r_contin;
 run;

* compute proportion of binary, std of contin, and n *;
proc means data=&out noprint;
 var &binary &contin;
 output out=_temp_(keep=p stdy n) mean=p std=stdx stdy n=n;
 run;

* sort by the binary variable *;
proc sort data=&out;
 by descending &binary;
 run;

* compute mean of contin and rank of contin var *;
proc means data=&out noprint;
 by notsorted &binary;
 var &contin r_contin;
 output out=&out mean=my r_contin;
 run;

* restructure the means computed in the step above *;
proc transpose data=&out out=&out(rename=(col1=my1 col2=my0));
 var r_contin my;
 run;

* combine the data needed to compute biserial correlation *;
data &out;
 set &out(drop= _name_ _label_);
 retain r1 r0 ;
 if _n_=1 then do;
  r1=my1;
  r0=my0;
 end;
 else do;
  set _temp_;
  output;
 end;
 run;

* compute point biserial correlation *;
proc corr data=&data  noprint outp=_temp_;
 var &binary &contin;
 run;



* extract the point biserial correlation from the matrix *;
data _temp_(keep=pntbisrl);
 set _temp_(rename=(&contin=pntbisrl));
 if _TYPE_='CORR' and &binary<>1 then output;

 run;

options notes;
* compute biserial and rank biserial *;
data &out;
 merge _temp_  &out;
 if pntbisrl=1 then delete;
 h=probit(1-p);
 u=exp(-h*h/2)/sqrt(2*arcos(-1));
 biserial=p*(1-p)*(my1-my0)/stdy/u;
 rnkbisrl=2*(r1-r0)/n;

 keep biserial pntbisrl rnkbisrl;
 label biserial='Biserial Corr'
       pntbisrl='Point Biserial Corr'
       rnkbisrl='Rank Biserial Corr';
 run;

%mend;

%biserial(data=ex.ex19_16, contin=Y, binary=X, out=out19_16);

PROC PRINT DATA=out19_16 label;
	VAR pntbisrl;
RUN;

PROC IML;	
	RESET nolog;
	n=13;
	r_pb=0.59830;
	r2_pb=(r_pb)**2;
	t=round((r_pb/sqrt((1-r2_pb)/(n-2))), 0.001);
	p_value = round((1 - probt(t, n-2))*2, 0.001);
	PRINT t p_value;
RUN;
QUIT;

SAS 출력

Concordance Correlation Coefficient


OBS	Point Biserial Corr
1	0.59830

Concordance Correlation Coefficient

t	p_value
2.476	0.031

EXAMPLE 19.17

PROC IML;	
    RESET nolog;
	sst=220.17; ssb=198.31;sse=21.86;
	df_b=6;df_e=7;
	msb=ssb/df_b;
	mse=sse/df_e;

	r=((msb-mse)/(msb+mse));
	f=msb/mse;

	p=1-probf(f,df_b,df_e);

	PRINT r f p;
RUN;
QUIT;

SAS 출력

Concordance Correlation Coefficient

r	f	p
0.8273449	10.583791	0.003251

EXAMPLE 19.18

PROC MEANS DATA=ex.ex19_18 noprint;
	VAR A B;
	OUTPUT OUT=dice_baselinemin min=var1 var2;
RUN;

proc means data=ex.ex19_18 noprint;
	VAR A B;
	OUTPUT OUT=dice_baselinemax max=var1 var2;
RUN;

DATA dice_baselineall;
	SET dice_baselinemin dice_baselinemax;
	DROP _type_ _freq_;
	IF _N_=1 THEN var1=floor(min(var1,var2));
	IF _N_=1 THEN var2=floor(min(var1,var2));
	IF _N_=2 THEN var1=ceil(max(var1,var2));	
	IF _N_=2 THEN var2=ceil(max(var1,var2));
RUN;

DATA dice_baselineall;
	SET ex.ex19_18 dice_baselineall;
RUN;

PROC GPLOT UNIFORM DATA=dice_baselineall;
plot A*B var1*var2/overlay vaxis=axis1 haxis=axis2 nolegend frame;
axis1 label=(a=90 'Cortisol Every Hour') minor=none;
axis2 label=('Cortisol Every Two Hours') minor=none;
symbol1 value=star color=black interpol=none;
symbol2 value=none color=black interpol=join;
title "Concordance Correlation Coefficient";
RUN;


PROC IML;
*******************************************************************************
  *  Enter the appropriate SAS data set name in the use statement and enter the *
  *  appropriate variable names in the read statements.                         *
  *******************************************************************************;
use ex.ex19_18;
read all var {A} into var1;
read all var {B} into var2;
*******************************************************************************
*  The IML module, labeled concorr, starts next.                              *
*******************************************************************************;
start concorr;
nonmiss=loc(var1#var2^=.);
var1=var1[nonmiss];
var2=var2[nonmiss];
free nonmiss;
n=nrow(var1);
mu1=sum(var1)/n;
mu1=round(mu1,0.0001);
mu2=sum(var2)/n;
mu2=round(mu2,0.0001);
sigma11=ssq(var1-mu1)/(n-1);
sigma11=round(sigma11,0.0001);
sigma22=ssq(var2-mu2)/(n-1);
sigma22=round(sigma22,0.0001);
sigma12=sum((var1-mu1)#(var2-mu2))/(n-1);
sigma12=round(sigma12,0.0001);
lshift=(mu1-mu2)/((sigma11#sigma22)##0.25);
rho=sigma12/sqrt(sigma11#sigma22);
rho=round(rho,0.0001);
z=log((1+rho)/(1-rho))/2;
se_z=1/sqrt(n-3);
t=tinv(0.975,n-3);
z_low=z-(se_z#t);
z_upp=z+(se_z#t);
rho_low=(exp(2#z_low)-1)/(exp(2#z_low)+1);
rho_low=round(rho_low,0.0001);
rho_upp=(exp(2#z_upp)-1)/(exp(2#z_upp)+1);
rho_upp=round(rho_upp,0.0001);
crho=(2#sigma12)/((sigma11+sigma22)+((mu1-mu2)##2));
crho=round(crho,0.0001);
z=log((1+crho)/(1-crho))/2;
if sigma12^=0 then do;
   t1=((1-(rho##2))#(crho##2))/((1-(crho##2))#(rho##2));
   t2=(2#(crho##3)#(1-crho)#(lshift##2))/(rho#((1-(crho##2))##2));
   t3=((crho##4)#(lshift##4))/(2#(rho##2)#((1-(crho##2))##2));
   se_z=sqrt((t1+t2-t3)/(n-2));
end;
else se_z=sqrt(2#sigma11#sigma22)/((sigma11+sigma22+((mu1-mu2)##2))#(n-2));
t=tinv(0.975,n-2);
z_low=z-(se_z#t);
z_upp=z+(se_z#t);
crho_low=(exp(2#z_low)-1)/(exp(2#z_low)+1);
crho_low=round(crho_low,0.0001);
crho_upp=(exp(2#z_upp)-1)/(exp(2#z_upp)+1);
crho_upp=round(crho_upp,0.0001);
Results=n//mu1//mu2//sigma11//sigma22//sigma12//rho_low//rho//rho_upp//
        crho_low//crho//crho_upp;
r_name={'SampleSize' 'Mean_1' 'Mean_2' 'Variance_1' 'Variance_2' 'Covariance' 'Corr LowerCL'
       'Corr' 'Corr UpperCL' 'ConcCorr LowerCL' 'ConcCorr' 'ConcCorr UpperCL'};
print 'The Estimated Correlation and Concordance Correlation (and 95% Confidence Limits)';
print Results [rowname=r_name];
finish concorr;
*******************************************************************************
*  The IML module, labeled concorr, is finished.                              *
*******************************************************************************;
RUN concorr;

SAS 출력

Concordance Correlation Coefficient

The Estimated Correlation and Concordance Correlation (and 95% Confidence Limits)


Results
SampleSize	11
Mean_1	0.3855
Mean_2	0.3336
Variance_1	0.0107
Variance_2	0.007
Covariance	0.0086
Corr LowerCL	0.9682
Corr	0.9937
Corr UpperCL	0.9988
ConcCorr LowerCL	0.6248
ConcCorr	0.8434
ConcCorr UpperCL	0.9394

교재: Biostatistical Analysis (5th Edition) by Jerrold H. Zar

**이 글은 22학년도 1학기 의학통계방법론 과제 자료들을 정리한 글 입니다.**

Simple Linear Correlation

R 프로그램 결과

19장

EXAMPLE 19.1a

EXAMPLE 19.1b

EXAMPLE 19.2

EXAMPLE 19.3

EXAMPLE 19.4

EXAMPLE 19.5a

EXAMPLE 19.5b

EXAMPLE 19.6

EXAMPLE 19.7

EXAMPLE 19.8

EXAMPLE 19.9

EXAMPLE 19.10

EXAMPLE 19.11

EXAMPLE 19.12

EXAMPLE 19.13

EXAMPLE 19.14

EXAMPLE 19.15

EXAMPLE 19.16

EXAMPLE 19.17

EXAMPLE 19.18

SAS 프로그램 결과

19장

EXAMPLE 19.1

EXAMPLE 19.2

EXAMPLE 19.3

EXAMPLE 19.4

EXAMPLE 19.5a

EXAMPLE 19.5b

EXAMPLE 19.6

EXAMPLE 19.7

EXAMPLE 19.8

EXAMPLE 19.9

EXAMPLE 19.10

EXAMPLE 19.11

EXAMPLE 19.12

EXAMPLE 19.13

EXAMPLE 19.14

EXAMPLE 19.15

EXAMPLE 19.16

EXAMPLE 19.17

EXAMPLE 19.18

Templates (for web app):

Error