[의학통계방법론] Ch16. Multivariate Analysis of Variance

05 May 2022 in Study log / Study / 의학통계방법론 on R, Sas, Blog, Jekyll, Jupyter, Data, Python

Multivariate Analysis of Variance
R 프로그램 결과
- 16장
  - EXAMPLE 16.1
SAS 프로그램 결과
- 16장
  - EXAMPLE 16.1

Multivariate Analysis of Variance

예제 데이터파일 Exam 16.1.sav 다운로드

R 프로그램 결과

R 접기/펼치기 버튼

패키지

설치된 패키지 접기/펼치기 버튼

getwd()

## [1] "C:/Biostat"

library("foreign")
library("dplyr")
library("kableExtra")
library("mvoutlier")
library("mvnormtest")
library("broom")
library("biotools")

16장

16장 연습문제 불러오기

ex16_1 <- read.spss('Exam 16.1.sav', to.data.frame=T)

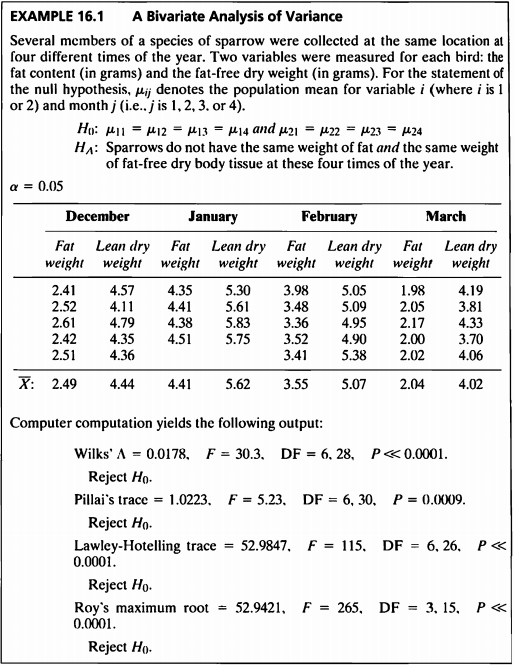
EXAMPLE 16.1

#데이터셋
ex16_1%>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
Y11	Y12	Y21	Y22	Y31	Y32	Y41	Y42
2.41	4.57	4.35	5.30	3.98	5.05	1.98	4.19
2.52	4.11	4.41	5.61	3.48	5.09	2.05	3.81
2.61	4.79	4.38	5.83	3.36	4.95	2.17	4.33
2.42	4.35	4.51	5.75	3.52	4.90	2.00	3.70
2.51	4.36	NA	NA	3.41	5.38	2.02	4.06

분석을 위하여 데이터를 정제하도록 하겠다.

month <- c(rep("December",5),rep("January",5),rep("February",5),rep("March",5))

fat <- c(ex16_1$Y11,ex16_1$Y21,ex16_1$Y31,ex16_1$Y41) 

lean <- c(ex16_1$Y12,ex16_1$Y22,ex16_1$Y32,ex16_1$Y42)

ex16 <- data.frame(month,fat,lean)

ex16%>%
  kbl(caption = "Dataset of Example 16.1") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset of Example 16.1
month	fat	lean
December	2.41	4.57
December	2.52	4.11
December	2.61	4.79
December	2.42	4.35
December	2.51	4.36
January	4.35	5.30
January	4.41	5.61
January	4.38	5.83
January	4.51	5.75
January	NA	NA
February	3.98	5.05
February	3.48	5.09
February	3.36	4.95
February	3.52	4.90
February	3.41	5.38
March	1.98	4.19
March	2.05	3.81
March	2.17	4.33
March	2.00	3.70
March	2.02	4.06

해당 데이터는 참새들의 지방 함량를 측정한 데이터로 같은 장소에서 4번씩 12월, 1월, 2월, 3월 이렇게 측정되었으며 지방에 따라 Fat weight와 Lean dry weight로 나뉜 데이터이다.
이 데이터를 사용하여 그룹별로 지방 함량의 평균이 같은지 알아보기 위해 다변량 분산분석을 시행해보고자 한다.
본 검정의 가설은 다음과 같다.

\[\begin{aligned} H_0 &: \mu_{11}=\mu_{12}=\mu_{13}=\mu_{14} \ and \ \mu_{21}=\mu_{22}=\mu_{23}=\mu_{24} \\ H_A &: \ Sparrows \ do \ not \ have \ the \ same \ weight \ of \ fat \ and \ the \ same \ weight \ of \ fat-free \ dry \ body \ tissue \ at \ these \ four \ times \ of \ the \ year. \end{aligned}\]

우선 반복측정자료분석에서의 가정 (다변량적 접근)을 살펴보겠다.
- 종속변수들의 상관성
- 다변량 정규성 (multivariate normality)
  - 종속변수들은 다변량 정규분포를 따른다.
  - 종속변수들의 선형조합도 정규분포를 따른다.
- 분산-공분산 행렬의 동질성 (homogeneity)
  - MANOVA는 그룹내 분산-공분산 행렬이 동일하다고 가정한다.
  - 분산-공분산 행렬의 동질성은 Box의 M-test를 이용하여 확인한다.
- 선형성 (linearity): 종속변수들과 독립변수들 간 선형성
- 관측 벡터의 독립성 (independence): 각 개체들은 서로 독립
- 임의 표본 (random sampling)
다음은은 MANOVA에 대한 검정통계량을 살펴보겠다.
- Wilks’ lambda (윌크스의 람다)
  - 0과 1사이의 값으로 산출되며, 처리효과가 있을수록 값이 작아진다.
  - 만약 그룹 간 효과와 관련된 B(between)가 커지면 윌크스의 람다 값은 0에 가까워지고 만약 작아지면 1에 가까워진다.
    \(\Lambda=\frac{\mid W \mid }{\mid B+W \mid}=\frac{\mid W \mid}{\mid T \mid}=\prod_{i=1}^{q}\frac{1}{1+\lambda_i}\)
    \(where \ W \ and \ T \ are \ determinants \ of \ the \ within \ and \ total \ sum \ of \ squares \ and \ cross-product \ matrices\)
- Phillai’s trace (필라이 대각합)
  - 양수의 값을 가지며, 처리효과가 클수록 값이 커진다.
    \(trace[B(B+W)^{-1}]=\sum_{i=1}^{q}\frac{\lambda_i}{1+\lambda_i}\)
- Lawley-Hotelling trace (로리-호텔링의 대각합)
  - 양수의 값을 가지며, 효과가 있으면 값이 커진다.
    \(trace[BW^{-1}]=\sum_{i=1}^{q}\lambda_i\)
- Roy’s maximum root (로이의 최대근)
  - 양수의 값을 가지며, 효과가 있을수록 값이 커진다.
    \(max(\lambda_i)\)
데이터에 이상치가 존재하는지 확인하도록 하겠다.

library("mvoutlier")
aq.plot(na.omit(ex16[,2:3]),alpha=0.05)

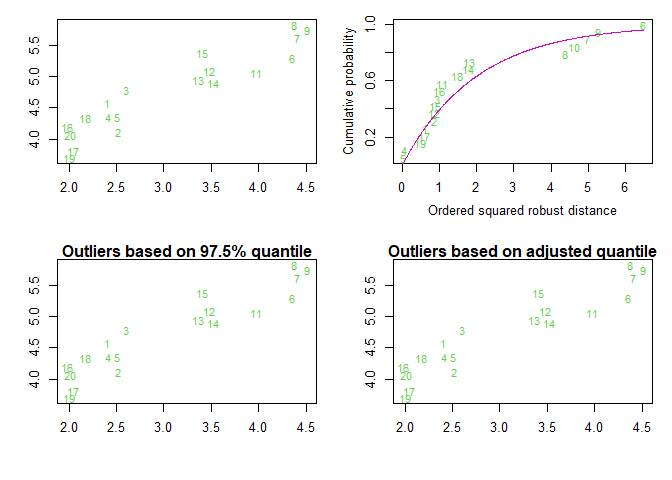
## $outliers
##     1     2     3     4     5     6     7     8     9    11    12    13    14 
## FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE 
##    15    16    17    18    19    20 
## FALSE FALSE FALSE FALSE FALSE FALSE

이상치가 없는 것으로 확인되며, 그룹별로 정규성을 따르는지 확인하도록 하겠다.

다변량 정규성 검정

library("mvnormtest") # mshapiro.test
library("broom") # tidy
mshapiro.test(t(ex16[1:5,2:3])) %>% tidy %>% 
  kable(,caption = "Normality test (December)") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Normality test (December)
statistic	p.value	method
0.79349	0.0716398	Shapiro-Wilk normality test

mshapiro.test(t(na.omit(ex16[6:10,2:3]))) %>% tidy %>% 
  kable(,caption = "Normality test (January)") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Normality test (January)
statistic	p.value	method
0.8272233	0.1606765	Shapiro-Wilk normality test

mshapiro.test(t(ex16[11:15,2:3])) %>% tidy %>% 
  kable(,caption = "Normality test (February)") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Normality test (February)
statistic	p.value	method
0.7764365	0.0513539	Shapiro-Wilk normality test

mshapiro.test(t(ex16[16:20,2:3])) %>% tidy %>% 
  kable(,caption = "Normality test (March)") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Normality test (March)
statistic	p.value	method
0.7946881	0.0732947	Shapiro-Wilk normality test

정규성 검정 결과 모든 p-value는 유의수준 0.05보다 크므로 정규성을 따른다는 귀무가설을 기각할 충한 근거가 없다.
그러므로 해당 데이터는 그룹별로 정규성을 따른다고 하겠다.
다음으로는 월 별로 공분산 행렬을 계산하여 보고, 공분산 행렬이 동질적인지 Box’s M test를 수행하도록 하겠다.

분산-공분산행렬 동질성 검정

ex16_na <- na.omit(ex16)
covm <- by(ex16_na[,2:3], ex16_na$month, cov)

covm$December %>% 
  kable(caption = "Covariance Matrices by December") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Covariance Matrices by December
	fat	lean
fat	0.00673	0.00662
lean	0.00662	0.06568

covm$January %>% 
  kable(caption = "Covariance Matrices by January") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Covariance Matrices by January
	fat	lean
fat	0.004825	0.0086250
lean	0.008625	0.0544917

covm$February %>% 
  kable(caption = "Covariance Matrices by February") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Covariance Matrices by February
	fat	lean
fat	0.061600	-0.006375
lean	-0.006375	0.035030

covm$March %>% 
  kable(caption = "Covariance Matrices by March") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Covariance Matrices by March
	fat	lean
fat	0.00563	0.01001
lean	0.01001	0.06827

library("biotools") # boxM

boxM(ex16_na[,2:3], ex16_na$month) %>% tidy %>% 
  rename("Chi-sq statistic"="statistic","df"="parameter") %>% 
  kable(caption = "Homogeneity of Covariance Matrices") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Homogeneity of Covariance Matrices
Chi-sq statistic	p.value	df	method
9.559461	0.3873108	9	Box’s M-test for Homogeneity of Covariance Matrices

Box’s M test의 결과 p-value=0.387로써 유의수준 5%하에 귀무가설을 기각하지 못한다.
따라서 그룹간 공분산 행렬이 동일하지 않다는 충분한 근거가 없으며, 구형성을 만족한다고 할 수 있다.
이제 위에서 소개했던 MANOVA에 대한 검정통계량을 적용하여 보겠다.

anov <- manova(cbind(fat,lean)~month, data=ex16_na)

tidy(anov,  test = "Wilks") %>% 
  rename("Wilk's Lambda"="wilks","F value"="statistic") %>% 
  kable(caption = "MANOVA using Wilk's Lambda",booktabs = TRUE, valign = 't') %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

MANOVA using Wilk’s Lambda
term	df	Wilk’s Lambda	F value	num.df	den.df	p.value
month	3	0.0177815	30.32966	6	28	0
Residuals	15	NA	NA	NA	NA	NA

tidy(anov) %>% rename("Pillai's trace"="pillai","F value"="statistic") %>% 
  kable(caption = "MANOVA using Pillai's trace",booktabs = TRUE, valign = 't') %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

MANOVA using Pillai’s trace
term	df	Pillai’s trace	F value	num.df	den.df	p.value
month	3	1.02229	5.227982	6	30	0.0008709
Residuals	15	NA	NA	NA	NA	NA

tidy(anov,  test = "Hotelling") %>% rename("Hotelling-Lawley trace"="hl","F value"="statistic") %>% 
  kable(caption = "MANOVA using Hotelling-Lawley trace",booktabs = TRUE, valign = 't') %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

MANOVA using Hotelling-Lawley trace
term	df	Hotelling-Lawley trace	F value	num.df	den.df	p.value
month	3	52.98465	114.8001	6	26	0
Residuals	15	NA	NA	NA	NA	NA

tidy(anov,  test = "Roy") %>% rename("Roy's maximum root"="roy","F value"="statistic") %>% 
  kable(caption = "MANOVA using Roy's maximum root",booktabs = TRUE, valign = 't') %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

MANOVA using Roy’s maximum root
term	df	Roy’s maximum root	F value	num.df	den.df	p.value
month	3	52.94209	264.7104	3	15	0
Residuals	15	NA	NA	NA	NA	NA

4가지 방법 모두 p-value가 유의수준 0.05보다 작은 값을 가지는 것을 볼 수 있다.
따라서 월별 모든 참새들의 fat weight와 lean dry weight가 다르다고 할 수 있다.
다변량 분산분석의 사후분석을 하기 위해 판별함수 분석을 수행하여 종속변수들이 그룹을 어떻게 분리하는지 파악하도록 하겠다.

사후분석

dfa <- lda(month~fat+lean,data=ex16_na)
dfa

## Call:
## lda(month ~ fat + lean, data = ex16_na)
## 
## Prior probabilities of groups:
##  December  February   January     March 
## 0.2631579 0.2631579 0.2105263 0.2631579 
## 
## Group means:
##             fat   lean
## December 2.4940 4.4360
## February 3.5500 5.0740
## January  4.4125 5.6225
## March    2.0440 4.0180
## 
## Coefficients of linear discriminants:
##           LD1      LD2
## fat  6.461863  2.72530
## lean 1.127769 -4.11224
## 
## Proportion of trace:
##    LD1    LD2 
## 0.9992 0.0008

Prior probabilities of groups를 보면 4개의 월별 모두 표본 크기가 같으므로 사전확률도 0.2631579로 같다.
첫번쨰 판별함수 LD1의 열을 보면 fat weight 와 lean dry weight의 효과를 같은 방향으로 구분한다.
두번쨰 판별함수 LD2의 열을 보면 fat weight 와 lean dry weight의 효과를 반대 방향으로 구분한다.
Proportion of trace를 보면 LD1은 전체 변동의 99.92%를, LD2는 전체 변동의 0.08%를 설명한다.
마지막으로 판별점수를 가지고 산점도를 그려 시각화하여 보겠다.

lda_df <- data.frame(
  month = ex16_na[, "month"],
  lda = predict(dfa)$x
)

library("ggplot2")
ggplot(lda_df) +
  geom_point(aes(x = lda.LD1, y = lda.LD2, color = month), size = 4) +
  theme_classic()

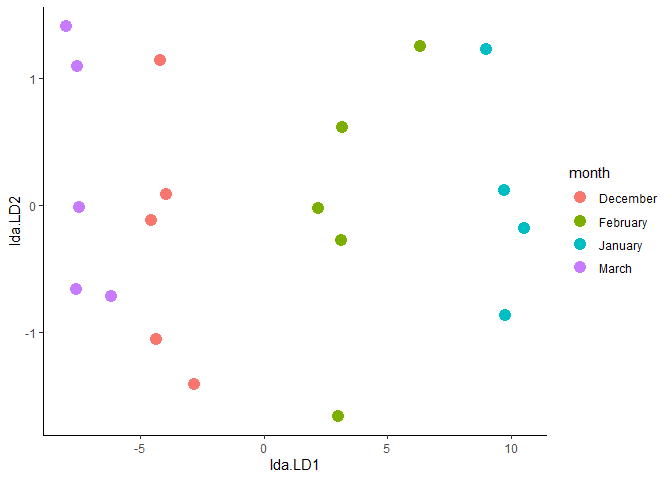
그래프를 보면 December과 March일 때의 판별점수가 February와 January와 확실히 significant하게 다름을 볼 수 있다.
December일 때와 March일 때가 매우 비슷하며 January 그룹에서 그룹별 지방함량의 평균이 같다는 귀무가설을 기각할 충분한 근거가 있는 효과 크기를 가지고 있다고 볼 수 있다.

SAS 프로그램 결과

SAS 접기/펼치기 버튼

16장

EXAMPLE 16.1

LIBNAME ex 'C:\Biostat';
RUN;

PROC IMPORT DBMS=sav
DATAFILE='C:\Biostat\Exam 16.1.sav'
OUT=ex.ex16_1 REPLACE;
RUN;

DATA ex.ex16_1x;
INPUT month $ w $ @@;
CARDS;
12 F 12 L
1 F 1 L
2 F 2 L
3 F 3 L
;
RUN;

PROC TRANSPOSE DATA=ex.ex16_1 OUT=ex.ex16_1a;
RUN;

DATA ex.ex16_1b;
	MERGE ex.ex16_1x ex.ex16_1a;
RUN; 

PROC SORT DATA=ex.ex16_1b;
	BY month;
RUN;

PROC TRANSPOSE DATA=ex.ex16_1b OUT=ex.ex16_1c (drop=_NAME_);
	BY month;
	ID w;
	VAR col1-col5;
RUN;

/*분산-공분산행렬 동질성 검정*/
PROC DISCRIM DATA=ex.ex16_1c POOL=test WCOV;
	CLASS month;
    VAR F L;
RUN;

SAS 출력

SAS 시스템

The DISCRIM Procedure


Total Sample Size	19	DF Total	18
Variables	2	DF Within Classes	15
Classes	4	DF Between Classes	3


Number of Observations Read	20
Number of Observations Used	19


Class Level Information
month	Variable Name	Frequency	Weight	Proportion	Prior Probability
1	1	4	4.0000	0.210526	0.250000
12	12	5	5.0000	0.263158	0.250000
2	2	5	5.0000	0.263158	0.250000
3	3	5	5.0000	0.263158	0.250000

SAS 시스템

The DISCRIM Procedure

Within-Class Covariance Matrices


month = 1, DF = 3
Variable	F	L
F	0.0048250000	0.0086250000
L	0.0086250000	0.0544916667


month = 12, DF = 4
Variable	F	L
F	0.0067300000	0.0066200000
L	0.0066200000	0.0656800000


month = 2, DF = 4
Variable	F	L
F	0.0616000000	-.0063750000
L	-.0063750000	0.0350300000


month = 3, DF = 4
Variable	F	L
F	0.0056300000	0.0100100000
L	0.0100100000	0.0682700000


Within Covariance Matrix Information
month	Covariance Matrix Rank	Natural Log of the Determinant of the Covariance Matrix
1	2	-8.57624
12	2	-7.82855
2	2	-6.15766
3	2	-8.16597
Pooled	2	-6.77867

SAS 시스템

The DISCRIM Procedure

Test of Homogeneity of Within Covariance Matrices


Chi-Square	DF	Pr > ChiSq
9.559461	9	0.3873

Since the Chi-Square value is not significant at the 0.1 level, a pooled covariance matrix will be used in the discriminant function.
Reference: Morrison, D.F. (1976) Multivariate Statistical Methods p252.

SAS 시스템

The DISCRIM Procedure


Generalized Squared Distance to month
From month	1	12	2	3
1	0	188.77724	38.34912	292.92415
12	188.77724	0	56.96520	11.66189
2	38.34912	56.96520	0	119.35753
3	292.92415	11.66189	119.35753	0


Linear Discriminant Function for month
Variable	1	12	2	3
Constant	-668.95259	-288.49311	-473.36844	-217.32186
F	194.98174	105.27489	154.71136	84.78096
L	84.93522	70.88157	78.34283	65.04515

SAS 시스템

The DISCRIM Procedure

Classification Summary for Calibration Data: EX.EX16_1C

Resubstitution Summary using Linear Discriminant Function


Number of Observations and Percent Classified into month
From month	1	12	2	3	Total
1	4 100.00	0 0.00	0 0.00	0 0.00	4 100.00
12	0 0.00	5 100.00	0 0.00	0 0.00	5 100.00
2	0 0.00	0 0.00	5 100.00	0 0.00	5 100.00
3	0 0.00	0 0.00	0 0.00	5 100.00	5 100.00
Total	4 21.05	5 26.32	5 26.32	5 26.32	19 100.00
Priors	0.25	0.25	0.25	0.25


Error Count Estimates for month
	1	12	2	3	Total
Rate	0.0000	0.0000	0.0000	0.0000	0.0000
Priors	0.2500	0.2500	0.2500	0.2500

ods graphics off;ods exclude all;ods noresults;
PROC GLM DATA=ex.ex16_1c;
	CLASS month;
	MODEL F L=month;
	MANOVA H=month;
	ODS OUTPUT OverallANOVA=OverallANOVA MultStat=MultStat;
RUN;
QUIT;
ods graphics on;ods exclude none;ods results;

PROC PRINT DATA=OverallANOVA;
RUN;

PROC PRINT DATA=MultStat;
RUN;

SAS 출력

SAS 시스템


OBS	Dependent	Source	DF	SS	MS	FValue	ProbF
1	F	Model	3	15.28045342	5.09348447	246.21	<.0001
2	F	Error	15	0.31031500	0.02068767	_	_
3	F	Corrected Total	18	15.59076842	_	_	_
4	L	Model	3	6.74124711	2.24708237	40.16	<.0001
5	L	Error	15	0.83939500	0.05595967	_	_
6	L	Corrected Total	18	7.58064211	_	_	_

SAS 시스템


OBS	Hypothesis	Error	Statistic	Value	FValue	NumDF	DenDF	ProbF	PValue
1	month	Error SSCP Matrix	Wilks' Lambda	0.01778151	30.33	6	28	<.0001	.
2	month	Error SSCP Matrix	Pillai's Trace	1.02229007	5.23	6	30	0.0009	.
3	month	Error SSCP Matrix	Hotelling-Lawley Trace	52.98465188	120.10	6	17	<.0001	.
4	month	Error SSCP Matrix	Roy's Greatest Root	52.94208549	264.71	3	15	<.0001	.

교재: Biostatistical Analysis (5th Edition) by Jerrold H. Zar

**이 글은 22학년도 1학기 의학통계방법론 과제 자료들을 정리한 글 입니다.**

Multivariate Analysis of Variance

R 프로그램 결과

16장

EXAMPLE 16.1

SAS 프로그램 결과

16장

EXAMPLE 16.1

Templates (for web app):

Error