[의학통계방법론] Ch13. Data Transformations

28 Apr 2022 in Study log / Study / 의학통계방법론 on R, Sas, Blog, Jekyll, Jupyter, Data, Python

Data Transformations
R 프로그램 결과
- 13장
SAS 프로그램 결과
- 13장

Data Transformations

예제 데이터파일 다운로드

R 프로그램 결과

R 접기/펼치기 버튼

패키지

설치된 패키지 접기/펼치기 버튼

getwd()

## [1] "C:/Biostat"

library("readxl")
library("dplyr")
library("kableExtra")

엑셀파일불러오기

#모든 시트를 하나의 리스트로 불러오는 함수
read_excel_allsheets <- function(file, tibble = FALSE) {
  sheets <- readxl::excel_sheets(file)
  x <- lapply(sheets, function(X) readxl::read_excel(file, sheet = X))
  if(!tibble) x <- lapply(x, as.data.frame)
  names(x) <- sheets
  x
}

13장

13장 연습문제 불러오기

#data_chap13에 연습문제 13장 모든 문제 저장
data_chap13 <- read_excel_allsheets("data_chap13.xls")

#연습문제 각각 데이터 생성
for (x in 1:length(data_chap13)){
  assign(paste0('ex13_',c(1:4))[x],data_chap13[x])
  }

#연습문제 데이터 형식을 리스트에서 데이터프레임으로 변환
for (x in 1:length(data_chap13)){
  assign(paste0('ex13_',c(1:4))[x],data.frame(data_chap13[x]))
  }

EXAMPLE 13.1

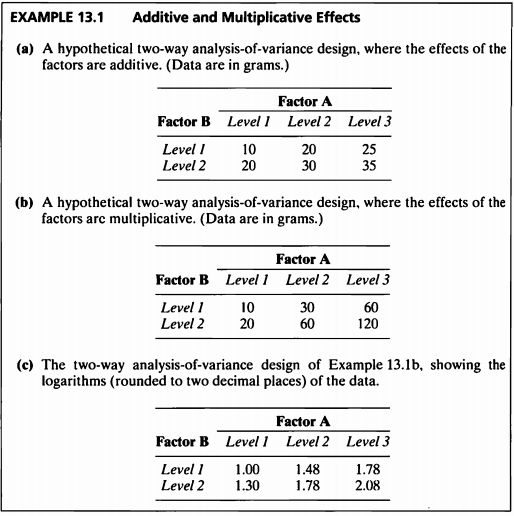
#데이터셋
ex13_1%>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
exam13_1.part	exam13_1.B	exam13_1.A	exam13_1.mean
1.	1	1	10.00
1.	2	1	20.00
1.	1	2	20.00
1.	2	2	30.00
1.	1	3	25.00
1.	2	3	35.00
1.	1	1	10.00
1.	2	1	20.00
1.	1	2	30.00
1.	2	2	60.00
1.	1	3	60.00
1.	2	3	120.00
1.	1	1	1.00
1.	2	1	1.30
1.	1	2	1.48
1.	2	2	1.78
1.	1	3	1.78
1.	2	3	2.08

해당 데이터는 a)와 multiplicate된 데이터 b)와 b)의 로그변환된 데이터 c)로 구성되어 있으며
세개의 데이터로 Interaction plot을 그려보고자 한다.

Interaction plot

par(mfrow=c(1,3))

interaction.plot(ex13_1[ex13_1$exam13_1.part=='a)',]$exam13_1.A,ex13_1[ex13_1$exam13_1.part=='a)',]$exam13_1.B,ex13_1[ex13_1$exam13_1.part=='a)',]$exam13_1.mean,bty="l",xlab="Factor A", ylab="mean", trace.label = "Factor B",main="Interaction plot of a)", las=1, type="b", pch=16, col=c("orange","#8f7450"))
interaction.plot(ex13_1[ex13_1$exam13_1.part=='a)',]$exam13_1.A,ex13_1[ex13_1$exam13_1.part=='a)',]$exam13_1.B,ex13_1[ex13_1$exam13_1.part=='b)',]$exam13_1.mean,bty="l",xlab="Factor A", ylab="mean", trace.label = "Factor B",main="Interaction plot of b)", las=1, type="b", pch=16, col=c("orange","#8f7450"))
interaction.plot(ex13_1[ex13_1$exam13_1.part=='a)',]$exam13_1.A,ex13_1[ex13_1$exam13_1.part=='a)',]$exam13_1.B,ex13_1[ex13_1$exam13_1.part=='c)',]$exam13_1.mean,bty="l",xlab="Factor A", ylab="mean", trace.label = "Factor B",main="Interaction plot of b)", las=1, type="b", pch=16, col=c("orange","#8f7450"))

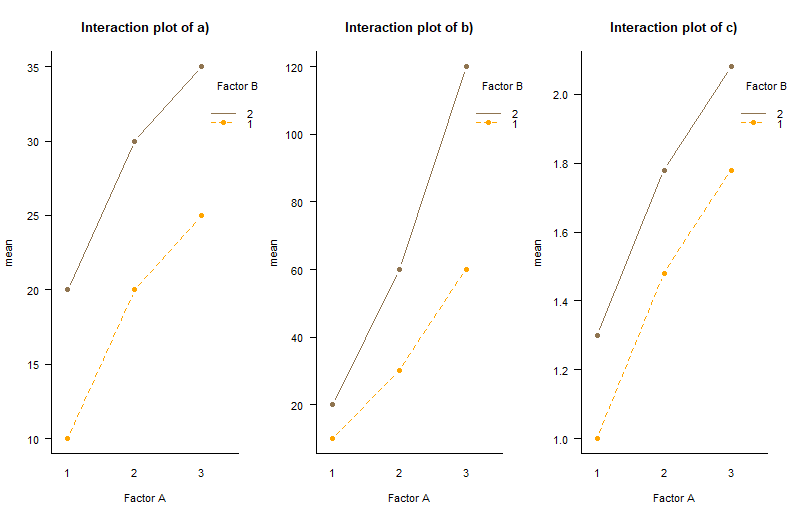
교호작용 그래프를 그려본 결과 위와 같은 결과가 나왔다.
a), b), c)의 경우 Factor A가 level 3이고 Factor B가 level 2 일 때 최대의 평균을 가지며
그 중 b)를 로그변환한 자료인 c)의 교호작용 그래프를 보면 보다 조금 더 추세적으로 안정화된 교호작용 그래프가 그려짐을 볼 수 있다.

EXAMPLE 13.2

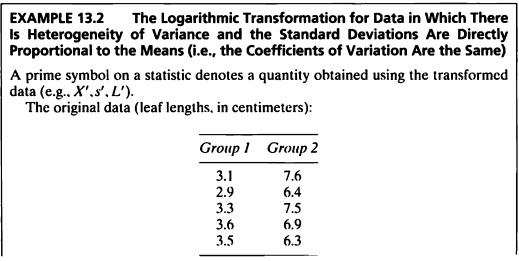
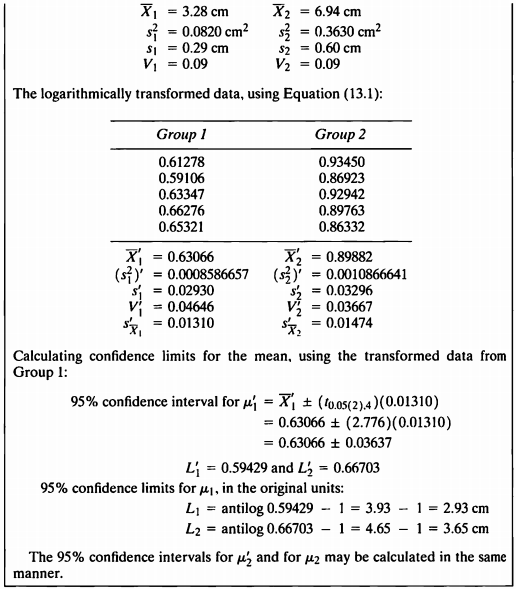
#데이터셋
ex13_2%>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
exam13_2.Group	exam13_2.Y
1	3.1
1	2.9
1	3.3
1	3.6
1	3.5
2	7.6
2	6.4
2	7.5
2	6.9
2	6.3

해당 데이터를 사용하여 로그변환을 고려해볼 것이다.
로그변환은 분산이 동질적이지 않으면서 표준편차는 평균에 비례적인 경우 사용할 수 있다.
original data를 로그변환한 데이터로 신뢰구간을 구하고, 그 값의 역로그변환을 하여 original data의 신뢰구간을 구하는 것도 볼 것이다.

Group1 <- subset(ex13_2$exam13_2.Y,ex13_2$exam13_2.Group==1)
Group2 <- subset(ex13_2$exam13_2.Y,ex13_2$exam13_2.Group==2)
ex13_2_split <- data.frame(Group1,Group2)
ex13_2_split%>%
  kbl(caption = "Dataset of Example 13.2") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset of Example 13.2
Group1	Group2
3.1	7.6
2.9	6.4
3.3	7.5
3.6	6.9
3.5	6.3

로그변환

\[\begin{aligned} X' = log_{10}(X+1) \end{aligned}\]

위 식을 사용하여 로그변환을 시도하겠다.

log_ex13_2 <- log10(ex13_2_split+1)
log_ex13_2%>%
  kbl(caption = "Logarithmic transformation of Example 13.2") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Logarithmic transformation of Example 13.2
Group1	Group2
0.6127839	0.9344985
0.5910646	0.8692317
0.6334685	0.9294189
0.6627578	0.8976271
0.6532125	0.8633229

parameter <- c("Mean","Variance","Std","CV")
f13_2 <- function(x){
  mean <- mean(x)
  s2 <- var(x)
  s <- round(sd(x),2)
  V <- round(sd(x)/mean(x),2)
  res <- list(mean,s2,s,V)
  return(res)
}

Group_1_original <- f13_2(ex13_2_split$Group1)
Group_2_original <- f13_2(ex13_2_split$Group2)

origin <- data.frame(cbind(parameter,Group_1_original,Group_2_original))

origin%>%
  kbl(caption = "Result of Original dataset") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Result of Original dataset
parameter	Group_1\_original	Group_2\_original
Mean	3.28	6.94
Variance	0.082	0.363
Std	0.29	0.6
CV	0.09	0.09

parameter <- c("Mean","Variance","Std","CV","s_p","Lower CI","Upper CI","Original Lower CI","Original Upper CI")
log_f13_2 <- function(x){
  mean <- mean(x)
  s2 <- var(x)
  s <- round(sd(x),4)
  V <- round(sd(x)/mean(x),2)
  s_p <- s/sqrt(length(x))
  L1_log <- round(mean(x)-((qt(1-(0.05/2), length(x)-1))*s_p), 5)
  L2_log <- round(mean(x)+((qt(1-(0.05/2), length(x)-1))*s_p), 5)
  L1_origin=round(10^(L1_log)-1, 2)
  L2_origin=round(10^(L2_log)-1, 2)
  res <- list(mean,s2,s,V,s_p,L1_log,L2_log,L1_origin,L2_origin)
  return(res)
}

Group_1_logtrans <- log_f13_2(log_ex13_2$Group1)
Group_2_logtrans <- log_f13_2(log_ex13_2$Group2)

logtrans <- data.frame(cbind(parameter,Group_1_logtrans,Group_2_logtrans))

logtrans%>%
  kbl(caption = "Result of logarithmic transformation dataset") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Result of logarithmic transformation dataset
parameter	Group_1\_logtrans	Group_2\_logtrans
Mean	0.6306575	0.8988198
Variance	0.0008585314	0.001086546
Std	0.0293	0.033
CV	0.05	0.04
s_p	0.01310336	0.01475805
Lower CI	0.59428	0.85784
Upper CI	0.66704	0.93979
Original Lower CI	2.93	6.21
Original Upper CI	3.65	7.71

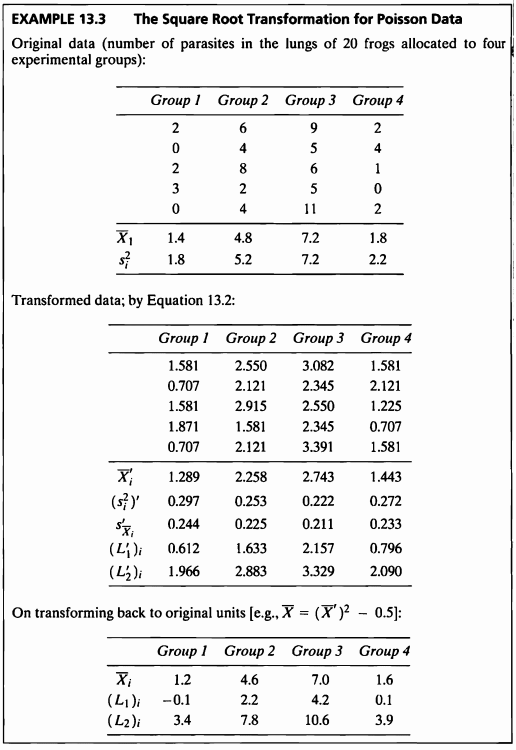
EXAMPLE 13.3

#데이터셋
ex13_3%>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
exam13_3.Group	exam13_3.Y
1	2
1	0
1	2
1	3
1	0
2	6
2	4
2	8
2	2
2	4
3	9
3	5
3	6
3	5
3	11
4	2
4	4
4	1
4	0
4	2

해당 데이터를 사용하여 제곱근변환을 고려해볼 것이다.
제곱근변환은 분산이 평균과 같이 증가하는 경향이 있는 경우, 포아송 분포를 따르는 데이터들 혹은 그룹의 분산이 평균들에 비례적일 경우 고려할 수 있다.

Group1 <- subset(ex13_3$exam13_3.Y,ex13_3$exam13_3.Group==1)
Group2 <- subset(ex13_3$exam13_3.Y,ex13_3$exam13_3.Group==2)
Group3 <- subset(ex13_3$exam13_3.Y,ex13_3$exam13_3.Group==3)
Group4 <- subset(ex13_3$exam13_3.Y,ex13_3$exam13_3.Group==4)
ex13_3_split <- data.frame(Group1,Group2,Group3,Group4)
ex13_3_split%>%
  kbl(caption = "Dataset of Example 13.3") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset of Example 13.3
Group1	Group2	Group3	Group4
2	6	9	2
0	4	5	4
2	8	6	1
3	2	5	0
0	4	11	2

제곱근변환

\[\begin{aligned} X^* = \sqrt{X+0.5} \end{aligned}\]

위 식을 사용하여 제곱근변환을 시도하겠다.

sqrt_ex13_3 <- sqrt(ex13_3_split+0.5)
sqrt_ex13_3%>%
  kbl(caption = "Sqruare root transformation of Example 13.3") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Sqruare root transformation of Example 13.3
Group1	Group2	Group3	Group4
1.5811388	2.549510	3.082207	1.5811388
0.7071068	2.121320	2.345208	2.1213203
1.5811388	2.915476	2.549510	1.2247449
1.8708287	1.581139	2.345208	0.7071068
0.7071068	2.121320	3.391165	1.5811388

parameter <- c("Mean","Variance","Std","Lower CI","Upper CI")
f13_3 <- function(x){
  mean <- mean(x)
  s2 <- var(x)
  s <- sd(x)
  L1 <- mean-(qt(0.975,4)*(s/sqrt(length(x))))
  L2 <- mean+(qt(0.975,4)*(s/sqrt(length(x))))
  res <- list(mean,s2,s,L1,L2)
  return(res)
}

Group_1_original <- f13_3(ex13_3_split$Group1)
Group_2_original <- f13_3(ex13_3_split$Group2)
Group_3_original <- f13_3(ex13_3_split$Group3)
Group_4_original <- f13_3(ex13_3_split$Group4)

origin <- data.frame(cbind(parameter,Group_1_original,Group_2_original,Group_3_original,Group_4_original))

origin%>%
  kbl(caption = "Result of Original dataset") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Result of Original dataset
parameter	Group_1\_original	Group_2\_original	Group_3\_original	Group_4\_original
Mean	1.4	4.8	7.2	1.8
Variance	1.8	5.2	7.2	2.2
Std	1.341641	2.280351	2.683282	1.48324
Lower CI	-0.2658671	1.96857	3.868266	-0.04168533
Upper CI	3.065867	7.63143	10.53173	3.641685

Group_1_sqrtrans <- f13_3(sqrt_ex13_3$Group1)
Group_2_sqrtrans <- f13_3(sqrt_ex13_3$Group2)
Group_3_sqrtrans <- f13_3(sqrt_ex13_3$Group3)
Group_4_sqrtrans <- f13_3(sqrt_ex13_3$Group4)

sqrtrans <- data.frame(cbind(parameter,Group_1_sqrtrans,Group_2_sqrtrans,Group_3_sqrtrans,Group_4_sqrtrans))

sqrtrans%>%
  kbl(caption = "Result of logarithmic transformation dataset") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Result of logarithmic transformation dataset
parameter	Group_1\_sqrtrans	Group_2\_sqrtrans	Group_3\_sqrtrans	Group_4\_sqrtrans
Mean	1.289464	2.257753	2.74266	1.44309
Variance	0.2966033	0.253189	0.2222736	0.2718643
Std	0.544613	0.5031789	0.471459	0.5214061
Lower CI	0.6132377	1.632974	2.157266	0.7956788
Upper CI	1.96569	2.882532	3.328053	2.090501

이렇게 변수변환 한 후에는 모수적 검정법을 적용하여 추후 분석을 진행할 수 있다.

EXAMPLE 13.4

#데이터셋
ex13_4%>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
exam13_4.Group	exam13_4.Y
1	84.2
1	88.9
1	89.2
1	83.4
1	80.1
1	81.3
1	85.8
2	92.3
2	95.1
2	90.3
2	88.6
2	92.6
2	96.0
2	93.7

해당 데이터를 사용하여 역싸인변환을 고려해볼 것이다.
역싸인변환은 이항형의 데이터 즉, 0~100% 까지의 퍼센티지 데이터 혹은 0과 1의 비율 데이터에 대해서 고려할 수 있다.

Group1 <- subset(ex13_4$exam13_4.Y,ex13_4$exam13_4.Group==1)
Group2 <- subset(ex13_4$exam13_4.Y,ex13_4$exam13_4.Group==2)
ex13_4_split <- data.frame(Group1,Group2)
ex13_4_split%>%
  kbl(caption = "Dataset of Example 13.4") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset of Example 13.4
Group1	Group2
84.2	92.3
88.9	95.1
89.2	90.3
83.4	88.6
80.1	92.6
81.3	96.0
85.8	93.7

역싸인변환

\[\begin{aligned} p^* &= arcsin \sqrt{p} \\ &=arcsin\sqrt{\frac{p}{100}} \times \frac{180}{\pi} \end{aligned}\]

위 식을 사용하여 역싸인변환을 시도하겠다.

arcsin_ex13_4 <- asin(sqrt(ex13_4_split/100))*(180/pi)
arcsin_ex13_4%>%
  kbl(caption = "Arcsine tranformation of Example 13.4") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Arcsine tranformation of Example 13.4
Group1	Group2
66.57851	73.88962
70.53891	77.21111
70.81414	71.85347
65.95645	70.26691
63.50664	74.21494
64.37781	78.46304
67.86261	75.46342

parameter <- c("Mean","Variance","Std","Lower CI","Upper CI")
f13_4 <- function(x){
  mean <- mean(x)
  s2 <- var(x)
  s <- sd(x)
  L1 <- mean-(qt(0.975,6)*(s/sqrt(length(x))))
  L2 <- mean+(qt(0.975,6)*(s/sqrt(length(x))))
  res <- list(mean,s2,s,L1,L2)
  return(res)
}

Group_1_original <- f13_4(ex13_4_split$Group1)
Group_2_original <- f13_4(ex13_4_split$Group2)

origin <- data.frame(cbind(parameter,Group_1_original,Group_2_original))

origin%>%
  kbl(caption = "Result of Original dataset") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Result of Original dataset
parameter	Group_1\_original	Group_2\_original
Mean	84.7	92.65714
Variance	12.29333	6.729524
Std	3.506185	2.594133
Lower CI	81.45732	90.25797
Upper CI	87.94268	95.05632

Group_1_arctrans <- f13_4(arcsin_ex13_4$Group1)
Group_2_arctrans <- f13_4(arcsin_ex13_4$Group2)

arctrans <- data.frame(cbind(parameter,Group_1_arctrans,Group_2_arctrans))

arctrans%>%
  kbl(caption = "Result of arcsine transformation dataset") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Result of arcsine transformation dataset
parameter	Group_1\_arctrans	Group_2\_arctrans
Mean	67.09072	74.48036
Variance	8.017362	8.226374
Std	2.831495	2.868166
Lower CI	64.47203	71.82775
Upper CI	69.70942	77.13297

SAS 프로그램 결과

SAS 접기/펼치기 버튼

13장

LIBNAME ex 'C:\Biostat';
RUN;

/*13장 연습문제 불러오기*/
%macro chap13(name=,no=);
%do i=1 %to &no.;
	PROC IMPORT DBMS=excel
		DATAFILE="C:\Biostat\data_chap13"
		OUT=ex.&name.&i. REPLACE;
		RANGE="exam13_&i.$";
	RUN;
%end;
%mend;

%chap13(name=ex13_,no=4);

EXAMPLE 13.1

DATA ex_13_1_a;
    SET ex.ex13_1;
    WHERE part = "a)";
RUN; 

DATA ex_13_1_b;
    SET ex.ex13_1;
    WHERE part = "b)";
RUN;

DATA ex_13_1_c;
    SET ex.ex13_1;
    WHERE part = "c)";
RUN; 

title "Example13.1";
PROC GLM DATA=ex_13_1_a;
    CLASS a b; 
    MODEL mean = a b a*b; 
RUN;

PROC GLM DATA=ex_13_1_b;
    CLASS a b; 
    MODEL mean = a b a*b; 
RUN;

PROC GLM DATA=ex_13_1_c;
    CLASS a b; 
    MODEL mean = a b a*b; 
RUN;

SAS 출력

Example13.1

The GLM Procedure


Class Level Information
Class	Levels	Values
A	3	1 2 3
B	2	1 2


Number of Observations Read	6
Number of Observations Used	6

Example13.1

The GLM Procedure

Dependent Variable: mean mean


Source	DF	Sum of Squares	Mean Square	F Value	Pr > F
Model	5	383.3333333	76.6666667	.	.
Error	0	0.0000000	.
Corrected Total	5	383.3333333


R-Square	Coeff Var	Root MSE	mean Mean
1.000000	.	.	23.33333


Source	DF	Type I SS	Mean Square	F Value	Pr > F
A	2	233.3333333	116.6666667	.	.
B	1	150.0000000	150.0000000	.	.
A*B	2	0.0000000	0.0000000	.	.


Source	DF	Type III SS	Mean Square	F Value	Pr > F
A	2	233.3333333	116.6666667	.	.
B	1	150.0000000	150.0000000	.	.
A*B	2	0.0000000	0.0000000	.	.

Example13.1

The GLM Procedure


Class Level Information
Class	Levels	Values
A	3	1 2 3
B	2	1 2


Number of Observations Read	6
Number of Observations Used	6

Example13.1

The GLM Procedure

Dependent Variable: mean mean


Source	DF	Sum of Squares	Mean Square	F Value	Pr > F
Model	5	8000.000000	1600.000000	.	.
Error	0	0.000000	.
Corrected Total	5	8000.000000


R-Square	Coeff Var	Root MSE	mean Mean
1.000000	.	.	50.00000


Source	DF	Type I SS	Mean Square	F Value	Pr > F
A	2	5700.000000	2850.000000	.	.
B	1	1666.666667	1666.666667	.	.
A*B	2	633.333333	316.666667	.	.


Source	DF	Type III SS	Mean Square	F Value	Pr > F
A	2	5700.000000	2850.000000	.	.
B	1	1666.666667	1666.666667	.	.
A*B	2	633.333333	316.666667	.	.

Example13.1

The GLM Procedure


Class Level Information
Class	Levels	Values
A	3	1 2 3
B	2	1 2


Number of Observations Read	6
Number of Observations Used	6

Example13.1

The GLM Procedure

Dependent Variable: mean mean


Source	DF	Sum of Squares	Mean Square	F Value	Pr > F
Model	5	0.75420000	0.15084000	.	.
Error	0	0.00000000	.
Corrected Total	5	0.75420000


R-Square	Coeff Var	Root MSE	mean Mean
1.000000	.	.	1.570000


Source	DF	Type I SS	Mean Square	F Value	Pr > F
A	2	0.61920000	0.30960000	.	.
B	1	0.13500000	0.13500000	.	.
A*B	2	0.00000000	0.00000000	.	.


Source	DF	Type III SS	Mean Square	F Value	Pr > F
A	2	0.61920000	0.30960000	.	.
B	1	0.13500000	0.13500000	.	.
A*B	2	0.00000000	0.00000000	.	.

EXAMPLE 13.2

title "Example13.2";

PROC MEANS DATA=ex.ex13_2 MEAN STD VAR; 
    CLASS group;
    VAR Y;
RUN;

SAS 출력

Example13.2

MEANS 프로시저


분석 변수: Y Y
Group	관측값 수	평균	표준편차	분산
1	5	3.2800000	0.2863564	0.0820000
2	5	6.9400000	0.6024948	0.3630000

DATA ex13_2_log;
    SET ex.ex13_2;
    log_y=round(log10(y+1), 0.00001);
RUN;

PROC MEANS DATA=ex13_2_log MEAN STD VAR; 
    CLASS group;
    VAR log_y;
RUN;

SAS 출력

Example13.2

MEANS 프로시저


분석 변수: log_y
Group	관측값 수	평균	표준편차	분산
1	5	0.6306560	0.0293030	0.000858666
2	5	0.8988200	0.0329646	0.0010867

DATA log_g1;
 	SET ex13_2_log;
	WHERE group = 1;
RUN;

DATA log_g2;
 	SET ex13_2_log;
	WHERE group = 2;
RUN;

PROC IML;
	USE log_g1;
	READ all; 
	CLOSE log_g1;
    t=round(abs(quantile("t",0.05/2, 4)),0.001);
    L1_log = round(mean(log_y) -(t*0.01310), 0.00001);
    L2_log = round(mean(log_y) +(t*0.01310), 0.00001);
    L1_origin=round((10**L1_log)-1, 0.01);
    L2_origin=round((10**L2_log)-1, 0.01);
print L1_log L2_log L1_origin L2_origin; 
RUN; 
QUIT;

SAS 출력

Example13.2

L1_log	L2_log	L1_origin	L2_origin
0.59429	0.66702	2.93	3.65

PROC IML;
	USE log_g2;
	READ all; 
	CLOSE log_g2;
    t=round(abs(quantile("t",0.05/2, 4)),0.001);
    L1_log = round(mean(log_y) -(t*0.01310), 0.00001);
    L2_log = round(mean(log_y) +(t*0.01310), 0.00001);
    L1_origin=round((10**L1_log)-1, 0.01);
    L2_origin=round((10**L2_log)-1, 0.01);
print L1_log L2_log L1_origin L2_origin; 
RUN;
QUIT;

SAS 출력

Example13.2

L1_log	L2_log	L1_origin	L2_origin
0.86245	0.93519	6.29	7.61

EXAMPLE 13.3

PROC TABULATE DATA=ex.ex13_3;
     CLASS Group;
     VAR Y;
     TABLE Y*(MEAN*F=6.1 VAR*F=6.1),  Group;
RUN;

SAS 출력

Example13.2


		Group
		1	2	3	4
Y	Mean	1.4	4.8	7.2	1.8
Y	Var	1.8	5.2	7.2	2.2

DATA ex13_3_eq13_2;
    SET ex.ex13_3;
    transY = sqrt(Y+0.5);
RUN;

PROC TABULATE DATA=ex13_3_eq13_2 out=ex13_3_out;
    CLASS Group;
    VAR transY;
    TABLE transY*(MEAN*F=6.3 VAR*F=6.3  lclm*F=6.3 uclm*F=6.3),  Group;
RUN;

SAS 출력

Example13.2


		Group
		1	2	3	4
transY	Mean	1.289	2.258	2.743	1.443
	Var	0.297	0.253	0.222	0.272
	95_LCLM	0.613	1.633	2.157	0.796
	95_UCLM	1.966	2.883	3.328	2.091

DATA ex13_3_original_unit;
    SET ex13_3_out;
    original_unit_mean = round( (transY_Mean)**2 - 0.5, 0.1);
    original_unit_LCLM = round( (transY_LCLM)**2 - 0.5, 0.1);
    original_unit_UCLM = round( (transY_UCLM)**2 - 0.5, 0.1);
RUN;

PROC PRINT DATA=ex13_3_original_unit;
    VAR Group original_unit_mean original_unit_LCLM original_unit_UCLM;
RUN;

SAS 출력

Example13.2


OBS	Group	original_unit_mean	original_unit_LCLM	original_unit_UCLM
1	1	1.2	-0.1	3.4
2	2	4.6	2.2	7.8
3	3	7.0	4.2	10.6
4	4	1.6	0.1	3.9

EXAMPLE 13.4

title "Example13.4";

PROC TABULATE DATA=ex.ex13_4;
    CLASS Group;
    VAR Y;
    TABLE Y*(MEAN*F=6.1 VAR*F=6.2 STD*F=6.1 lclm*F=6.2 uclm*F=6.2),  Group;
RUN;

SAS 출력

Example13.4


		Group
		1	2
Y	Mean	84.7	92.7
	Var	12.29	6.73
	Std	3.5	2.6
	95_LCLM	81.46	90.26
	95_UCLM	87.94	95.06

DATA exam13_4_trans;
    SET ex.ex13_4;
    pi=constant("PI") ; 
    transY=arsin(sqrt(Y/100))*(180/pi) ;
RUN;

PROC TABULATE DATA=exam13_4_trans;
    CLASS Group;
    VAR transY;
    TABLE transY*(MEAN*F=6.2 VAR*F=6.4 STD*F=6.2 lclm*F=6.2 uclm*F=6.2),  Group;
RUN;

SAS 출력

Example13.4


		Group
		1	2
transY	Mean	67.09	74.48
	Var	8.0174	8.2264
	Std	2.83	2.87
	95_LCLM	64.47	71.83
	95_UCLM	69.71	77.13

교재: Biostatistical Analysis (5th Edition) by Jerrold H. Zar

**이 글은 22학년도 1학기 의학통계방법론 과제 자료들을 정리한 글 입니다.**

Data Transformations

R 프로그램 결과

13장

EXAMPLE 13.1

EXAMPLE 13.2

EXAMPLE 13.3

EXAMPLE 13.4

SAS 프로그램 결과

13장

EXAMPLE 13.1

EXAMPLE 13.2

EXAMPLE 13.3

EXAMPLE 13.4

Templates (for web app):

Error