[의학통계방법론] Ch9. Paired-Sample Hypotheses

31 Mar 2022 in Study log / Study / 의학통계방법론 on R, Sas, Blog, Jekyll, Jupyter, Data, Python

• Paired-Sample Hypotheses
• R 프로그램 결과
  • 9장
    • EXAMPLE 9.1
    • EXAMPLE 9.2
    • EXAMPLE 9.3
    • EXAMPLE 9.4
• SAS 프로그램 결과
  • 9장
    • EXAMPLE 9.1
    • EXAMPLE 9.2
    • EXAMPLE 9.3
    • EXAMPLE 9.4

Paired-Sample Hypotheses

예제 데이터파일 다운로드

R 프로그램 결과

R 접기/펼치기 버튼

패키지

설치된 패키지 접기/펼치기 버튼

getwd()

## [1] "C:/Biostat"

library("readxl")
library("dplyr")
library("kableExtra")
library("PairedData")

엑셀파일불러오기

#모든 시트를 하나의 리스트로 불러오는 함수
read_excel_allsheets <- function(file, tibble = FALSE) {
  sheets <- readxl::excel_sheets(file)
  x <- lapply(sheets, function(X) readxl::read_excel(file, sheet = X))
  if(!tibble) x <- lapply(x, as.data.frame)
  names(x) <- sheets
  x
}

9장

9장 연습문제 불러오기

#data_chap09에 연습문제 9장 모든 문제 저장
data_chap09 <- read_excel_allsheets("data_chap09.xls")

#연습문제 각각 데이터 생성
for (x in 1:length(data_chap09)){
  assign(paste0('ex9_',1:length(data_chap09))[x],data_chap09[x])
  }

#연습문제 데이터 형식을 리스트에서 데이터프레임으로 변환
for (x in 1:length(data_chap09)){
  assign(paste0('ex9_',1:length(data_chap09))[x],data.frame(data_chap09[x]))
  }

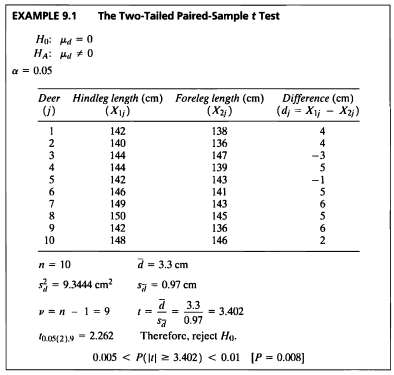
EXAMPLE 9.1

#데이터셋
ex9_1%>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset

exam9_1.deer	exam9_1.hindleg	exam9_1.foreleg
1	142	138
2	140	136
3	144	147
4	144	139
5	142	143
6	146	141
7	149	143
8	150	145
9	142	136
10	148	146

• 해당 데이터는 사슴의 앞 다리와 뒷 다리에 대한 데이터로써 서로 짝을 이룬 대응표본 데이터이다.
  
• 사슴 모집단의 앞 다리 길이와 뒷 다리 길이의 차이가 있는지 검정하고자 한다.

\[\begin{aligned} H_0 &: \mu_d = 0 \\ H_A &: \mu_d \not=\ 0 \end{aligned}\]

• 서로 짝을 이룬 데이터이므로 Paired Sample t-test를 시행할 수 있으며, 앞 다리와 뒷 다리의 차이를 모수로 두어 One Sample t-test를 시행할 수도 있다.
  
• Paired Sample t-test의 경우 정규성을 만족해야하는 가정이 있으므로 정규성 검정을 시행한다.

표본의 크기가 작으므로 Shapiro-Wilk test를 사용할 것이다.

ex9_1$diff <- ex9_1$exam9_1.hindleg-ex9_1$exam9_1.foreleg
shapiro.test(ex9_1$diff)

## 
##  Shapiro-Wilk normality test
## 
## data:  ex9_1$diff
## W = 0.81366, p-value = 0.02123

• Paired Sample의 경우 정규성 가정시 두 표본에 대한 차이 값으로 정규성 검정을 시행하여야 한다.
  
• 정규성 검정의 결과 p-value = 0.02603으로써 정규성 가정을 만족하지 못하였으므로 비모수 검정을 시행하여야 하지만 비모수 검정은 EXAMPLE 9.4에서 다시 다루도록 하겠다.
  
• 이 예제에서는 Paired Sample t-test를 시행하여 보겠다.

t.test(ex9_1$exam9_1.hindleg,ex9_1$exam9_1.foreleg,mu=0,alt='two.sided', paired=T) # t.test(ex9_1$diff,mu=0,alt='two.sided') 같은 결과를 준다.

## 
##  Paired t-test
## 
## data:  ex9_1$exam9_1.hindleg and ex9_1$exam9_1.foreleg
## t = 3.4138, df = 9, p-value = 0.007703
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
##  1.113248 5.486752
## sample estimates:
## mean difference 
##             3.3

• 검정통계량 값이 3.4138 문제의 값인 3.402와 다르게 나온 이유는 두 표본에 대한 표준편차가 반올림을 해서 계산이 되었기 때문이다.
  
• 이 예제에서는 두 표본에 대한 표준편차 0.9666667를 소수점 셋째자리에서 반올림하였다.
  
• p-value = 0.007703이므로 유의수준 5%하에 귀무가설을 기각할 수 있다.
  
• 즉, 사슴 모집단의 앞 다리와 뒷 다리의 길이의 차이가 있다고 할 수 있다.

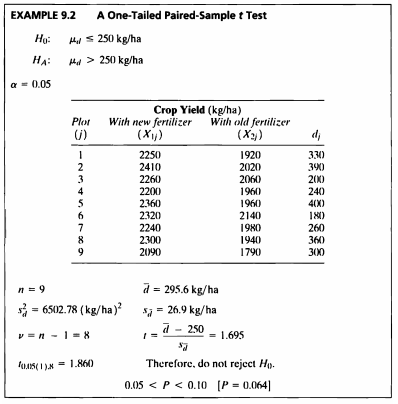
EXAMPLE 9.2

#데이터셋
ex9_2%>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset

exam9_2.plot	exam9_2.new	exam9_2.old	exam9_2.d
1	2250	1920	330
2	2410	2020	390
3	2260	2060	200
4	2200	1960	240
5	2360	1960	400
6	2320	2140	180
7	2240	1980	260
8	2300	1940	360
9	2090	1790	300

• 해당 데이터는 기존 비료와 새로운 비료에 따른 수확량을 기록한 데이터이다.
  
• 새로운 비료와 기존 비료의 곡물 수확량 차이 모평균에 대한 검정을 수행할 것이다.

\[\begin{aligned} H_0 &: \mu_d \leq25 kg/ha \\ H_A &: \mu_d>250kg/ha \end{aligned}\]

• Paired Sample t-test의 경우 정규성을 만족해야하는 가정이 있으므로 정규성 검정을 시행한다.

표본의 크기가 작으므로 Shapiro-Wilk test를 사용할 것이다.

shapiro.test(ex9_2$exam9_2.d)

## 
##  Shapiro-Wilk normality test
## 
## data:  ex9_2$exam9_2.d
## W = 0.94359, p-value = 0.6202

• p-value가 0.6202 이므로 유의수준 5%하에 두 집단 모두 정규성을 따르지 않는다고 할 충분한 증거가 없다.
  
• 따라서 정규성 가정을 만족한다 보고 Paired Sample t-test를 시행하겠다.

t.test(ex9_2$exam9_2.new, ex9_2$exam9_2.old, mu=250, alt='greater', paired=T) # t.test(ex9_2$exam9_2.d, mu=250, alt="greater")  같은 결과를 준다.

## 
##  Paired t-test
## 
## data:  ex9_2$exam9_2.new and ex9_2$exam9_2.old
## t = 1.6948, df = 8, p-value = 0.06428
## alternative hypothesis: true mean difference is greater than 250
## 95 percent confidence interval:
##  245.571     Inf
## sample estimates:
## mean difference 
##        295.5556

EXAMPLE 9.3

• 이 예제는 Example 9.1 데이터를 사용하여 모분산이 같은지에 대한 검정을 해보도록 할 것이다.

\[\begin{aligned} H_0 &: \sigma_1^2=\sigma_2^2 \\ H_A &: \sigma_1^2\neq\sigma_2^2 \end{aligned}\]

• 두개의 paired-samples에 대해 분산이 같은지 여부를 검증하기 위해 Pitman 검정을 진행했다.

직접 함수를 작성해서 구하여 보자.

v1=round(var(ex9_1$exam9_1.hindleg),2)
v2=round(var(ex9_1$exam9_1.foreleg),2)
r=cor(ex9_1$exam9_1.hindleg,ex9_1$exam9_1.foreleg)
F=round(v1/v2,4)
n=length(ex9_1$exam9_1.hindleg)
t=round(((F-1)*sqrt(n-2))/(2*sqrt(F*(1-r^2))),3)
t_0.05=round(qt(0.025, df=8, lower.tail=F),3)
cat("\t F=",F," t=",t," t_0.05=",t_0.05, "\n\t Therefore cannot reject null hypothesis")

##   F= 0.7111  t= -0.656  t_0.05= 2.306 
##   Therefore cannot reject null hypothesis

• t 값은 -0.656으로 자유도가 8인 t_0.05값 2.306보다 그 절대값이 작기 때문에 사슴 앞 다리의 길이와 사슴 뒷 다리의 길이의 모분산이 같다는 귀무가설을 기각할 수 없다.

다음은 PairedData 패키지의 pitman.morgan.test.default() 함수 사용

library(PairedData)
pitman.morgan.test.default(ex9_1$exam9_1.hindleg,ex9_1$exam9_1.foreleg)

## 
##  Paired Pitman-Morgan test
## 
## data:  ex9_1$exam9_1.hindleg and ex9_1$exam9_1.foreleg
## t = -0.65591, df = 8, p-value = 0.5303
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.227042 2.226964
## sample estimates:
## variance of x variance of y 
##      11.56667      16.26667

• p-value가 0.5303으로 유의수준 5%하에 귀무가설을 기각할 수 없다.

Fisher의 방법으로 분산이 동일한지 검정

var.test(ex9_1$exam9_1.hindleg,ex9_1$exam9_1.foreleg,ratio=1,alternative = "two.sided",paired=T)

## 
##  F test to compare two variances
## 
## data:  ex9_1$exam9_1.hindleg and ex9_1$exam9_1.foreleg
## F = 0.71107, num df = 9, denom df = 9, p-value = 0.6197
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.1766186 2.8627458
## sample estimates:
## ratio of variances 
##          0.7110656

• p-value가 0.6197로 유의수준 5%하에 귀무가설을 기각할 수 없다.
  
• 따라서 유의수준 5%하에 사슴 앞 다리 길이와 뒷 다리 길이의 모분산이 다르다고 말할만한 충분한 근거가 없다.

EXAMPLE 9.4

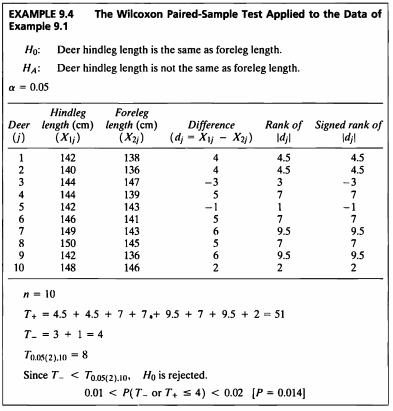
• 이 예제에서는 Example 9.1 데이터가 정규성 가정을 만족하지 못하였으므로 비모수 검정을 시행하여보겠다.

\[\begin{aligned} H_0:\ Deer\ hindleg\ length\ is\ the\ same\ as\ foreleg\ length.\\ H_A: eer\ hind\ leg\ length\ is\ not\ the\ same\ as\ forele\ length. \end{aligned}\]

ex9_1$diff=ex9_1$exam9_1.hindleg-ex9_1$exam9_1.foreleg
ex9_1$d.rank= rank(abs(ex9_1$diff))
ex9_1$sign_rank= ifelse(ex9_1$diff < 0, ex9_1$d.rank *(-1), ex9_1$d.rank) 
T.plus= sum(subset(ex9_1, sign_rank>=0)$sign_rank)
T.minus= abs(sum(subset(ex9_1, sign_rank< 0)$sign_rank)) 

T.plus;T.minus

## [1] 51

## [1] 4

• signed rank의 양수 합은 51, 음수 합은 4이다.
  
• 대응 표본에 대하여 비모수 검정법인 Wilcoxon signed rank test 수행하였다.

wilcox.test(ex9_1$exam9_1.hindleg, ex9_1$exam9_1.foreleg, paired=T)

## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  ex9_1$exam9_1.hindleg and ex9_1$exam9_1.foreleg
## V = 51, p-value = 0.01859
## alternative hypothesis: true location shift is not equal to 0

• p유의수준 5%에서 기각역은 8이다.
  
• 4 < 8이므로 귀무가설을 기각하고 대립가설을 채택한다.
  
• 즉. 유의수준 5% 하에서 사슴 앞다리 길이의 모평균과 뒷다리 길이의 모평균은 다르다고 볼 수 있는 충분한 근거가 있다.

SAS 프로그램 결과

SAS 접기/펼치기 버튼

9장

LIBNAME ex 'C:\Biostat';
RUN;

/*9장 연습문제 불러오기*/
%macro chap09(name=,no=);
%do i=1 %to &no.;
	PROC IMPORT DBMS=excel
		DATAFILE="C:\Biostat\data_chap09"
		OUT=ex.&name.&i. REPLACE;
		RANGE="exam9_&i.$";
	RUN;
%end;
%mend;

%chap09(name=ex9_,no=2);

EXAMPLE 9.1

DATA ex9_1_diff;
    SET ex.ex9_1;
    diff=hindleg-foreleg;
    abs_diff = abs(diff);
RUN;

ods graphics off;ods exclude all;ods noresults;
PROC UNIVARIATE DATA=ex9_1_diff normal;
    VAR diff;
ods output TestsForNormality = TestsForNormality;
RUN;

PROC TTEST DATA=ex.ex9_1;
	PAIRED hindleg * foreleg ;
    ods output TTests =TTests;
RUN;
ods graphics on;ods exclude none;ods results;

PROC SORT DATA=TestsForNormality;
    BY descending Test;
RUN;
title 'Example 9.1: 정규성검정';
PROC PRINT DATA=TestsForNormality label;
RUN;
title 'Example 9.1: Two-Tailed Paired-Sample t Test';
PROC PRINT DATA=TTests label;
RUN;

Example 9.1: 정규성검정

OBS	VarName	적합도 검정	적합도 통계량에 대한 레이블	적합도 통계량 값	p-값 레이블	p-값의 부호	p-값
1	diff	Shapiro-Wilk	W	0.813656	Pr < W		0.0212
2	diff	Kolmogorov-Smirnov	D	0.290563	Pr > D		0.0177
3	diff	Cramer-von Mises	W-Sq	0.150917	Pr > W-Sq		0.0198
4	diff	Anderson-Darling	A-Sq	0.831819	Pr > A-Sq		0.0213

---

Example 9.1: Two-Tailed Paired-Sample t Test

OBS	Variable 1	Variable 2	Difference	t Value	DF	Pr > |t|
1	hindleg	foreleg	hindleg - foreleg	3.41	9	0.0077

EXAMPLE 9.2

ods graphics off;ods exclude all;ods noresults;
PROC UNIVARIATE DATA=ex.ex9_2 normal;
    VAR d;
ods output TestsForNormality = TestsForNormality;
RU;
PROC TTEST order=data h0=250 SIDES=u
	DATA=ex.ex9_2;
	PAIRED new * old ;
    ods output TTests =TTests;
RUN;
ods graphics on;ods exclude none;ods results;

PROC SORT DATA=TestsForNormality;
 BY descending Test;
RUN;
title 'Example 9.2: 정규성검정';
PROC PRINT DATA=TestsForNormality label;
run;
title 'Example 9.2: One-Tailed Paired-Sample t Test';
PROC PRINT DATA=TTests label;
RUN;

Example 9.2: 정규성검정

OBS	VarName	적합도 검정	적합도 통계량에 대한 레이블	적합도 통계량 값	p-값 레이블	p-값의 부호	p-값
1	d	Shapiro-Wilk	W	0.94359	Pr < W		0.6202
2	d	Kolmogorov-Smirnov	D	0.121236	Pr > D	>	0.1500
3	d	Cramer-von Mises	W-Sq	0.028216	Pr > W-Sq	>	0.2500
4	d	Anderson-Darling	A-Sq	0.21151	Pr > A-Sq	>	0.2500

---

Example 9.2: One-Tailed Paired-Sample t Test

OBS	Variable 1	Variable 2	Difference	t Value	DF	Pr > t
1	new	old	new - old	1.69	8	0.0643

EXAMPLE 9.3

PROC IML;
    use ex.ex9_1 ; read all;
    n=10;
    s1=var(hindleg); 
	s2=var(foreleg);
	F=s1/s2;
	r=0.6739;
	t=((F-1)*sqrt(n-2))/(2*sqrt(F*(1-(r*r))));
	p=probt(-0.655, 8)*2;
PRINT F t p;
RUN;
QUIT;

Example 9.2: One-Tailed Paired-Sample t Test

F	t	p
0.7110656	-0.655872	0.530846

EXAMPLE 9.4

ods graphics off;ods exclude all;ods noresults;
PROC UNIVARIATE DATA=ex9_1_diff;
     VAR diff;
ods output TestsForLocation = TestsForLocation;
RUN;
ods graphics on;ods exclude none;ods results;
PROC PRINT DATA=TestsForLocation label;
RUN;

Example 9.2: One-Tailed Paired-Sample t Test

OBS	VarName	위치모수 검정	검정 통계량 레이블	검정 통계량	P-값 설명	P-값	Mu0 값
1	diff	스튜던트의 t	t	3.413793	Pr > |t|	0.0077	0
2	diff	부호	M	3	Pr >= |M|	0.1094	0
3	diff	부호 순위	S	23.5	Pr >= |S|	0.0117	0

PROC RANK DATA=ex9_1_diff out=ex9_1_rank;
    VAR abs_diff;
	RANKS rank;
RUN;
DATA ex9_1_signed_rank;
	SET ex9_1_rank;
	if diff < 0 then signed_rank = rank*(-1);
	else if diff > 0 then  signed_rank = rank;
RUN;
PROC PRINT DATA=ex9_1_signed_rank;
RUN;

PROC IML;
	use ex9_1_signed_rank;
	read all;
	close ex9_1_signed_rank;
		n = nrow(deer);
		plus = loc(diff>0);
		minus = loc(diff<0);
		rank_plus = rank[plus];
		rank_minus = rank[minus];
		T_plus = sum(rank_plus);
		T_minus = sum(rank_minus);
	PRINT T_plus T_minus ;
RUN;
QUIT;

Example 9.2: One-Tailed Paired-Sample t Test

OBS	deer	hindleg	foreleg	diff	abs_diff	rank	signed_rank
1	1	142	138	4	4	4.5	4.5
2	2	140	136	4	4	4.5	4.5
3	3	144	147	-3	3	3.0	-3.0
4	4	144	139	5	5	7.0	7.0
5	5	142	143	-1	1	1.0	-1.0
6	6	146	141	5	5	7.0	7.0
7	7	149	143	6	6	9.5	9.5
8	8	150	145	5	5	7.0	7.0
9	9	142	136	6	6	9.5	9.5
10	10	148	146	2	2	2.0	2.0

---

Example 9.2: One-Tailed Paired-Sample t Test

T_plus	T_minus
51	4

교재: Biostatistical Analysis (5th Edition) by Jerrold H. Zar

**이 글은 22학년도 1학기 의학통계방법론 과제 자료들을 정리한 글 입니다.**