[의학통계방법론] Ch8. Two-Sample Hypotheses

31 Mar 2022 in Study log / Study / 의학통계방법론 on R, Sas, Blog, Jekyll, Jupyter, Data, Python

Two-Sample Hypotheses
R 프로그램 결과
- 8장
SAS 프로그램 결과
- 8장

Two-Sample Hypotheses

예제 데이터파일 다운로드

R 프로그램 결과

R 접기/펼치기 버튼

패키지

설치된 패키지 접기/펼치기 버튼

getwd()

## [1] "C:/Biostat"

library("readxl")
library("dplyr")
library("asht")
library("lawstat") 
library("kableExtra")
library("qpcR")   
library("RVAideMemoire")
library("vegan")
library("gmodels")

엑셀파일불러오기

#모든 시트를 하나의 리스트로 불러오는 함수
read_excel_allsheets <- function(file, tibble = FALSE) {
  sheets <- readxl::excel_sheets(file)
  x <- lapply(sheets, function(X) readxl::read_excel(file, sheet = X, na = "."))
  if(!tibble) x <- lapply(x, as.data.frame)
  names(x) <- sheets
  x
}

8장

8장 연습문제 불러오기

#data_chap08에 연습문제 8장 모든 문제 저장
data_chap08 <- read_excel_allsheets("data_chap08.xls")

#연습문제 각각 데이터 생성
for (x in 1:length(data_chap08)){
  assign(paste0('ex8_',c(1:2,'2a',7:8,10:11))[x],data_chap08[x])
  }

#연습문제 데이터 형식을 리스트에서 데이터프레임으로 변환
for (x in 1:length(data_chap08)){
  assign(paste0('ex8_',c(1:2,'2a',7:8,10:11))[x],data.frame(data_chap08[x]))
  }

EXAMPLE 8.1

#데이터셋
ex8_1%>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
exam8_1.drug	exam8_1.time
B	8.8
B	8.4
B	7.9
B	8.7
B	9.1
B	9.6
C	9.9
C	9.0
C	11.1
C	9.6
C	8.7
C	10.4
C	9.5

약물 B를 투여했을 때 모든 성체 수컷 토끼의 혈액 응고 시간 평균이 약물 G를 투여했을 때 모든 성체 수컷 토끼의 혈액 응고 시간 평균이 다른지 검정하고자 한다.

\[\begin{aligned} H_0 &: \mu_1 = \mu_2 \\ H_A &: \mu_1 \not=\ \mu_2 \end{aligned}\]

성체 수컷 토끼 6마리에게 약물 B를 투여하였으며, 다른 성체 수컷 토끼 7마리에게 추출하여 두개의 표본은 독립적이게 추출하였다.
이표본 t-검정을 하기 전에 두 개의 표본분포의 정규성을 각각 보여야 하고 두 그룹 분포간 분산이 같은지 등분산성 가정을 확인해 줘야 한다.
정규성 검정은 P-P plot과 Q-Q plot으로도 정규성을 확인 할 수 있지만 그래프로 확인하는 정규성 검정은 기준이 모호하기 때문에 한계가 있다.
따라서 정규성에 대한 기타 평가 방법들을 사용할 것인데 표본의 크기가 작으므로 Shapiro-Wilk test를 사용할 것이다.
(표본크기가 매우 작으므로 웬만해선 정규성이 있는 것처럼 나올 것이다.)

##정규성,등분산성 검정
test <- function(x,y) {
  norm1 = shapiro.test(x)$p.value
  norm2 = shapiro.test(y)$p.value
  equal.var = var.test(x,y)$p.value 
  summary <- list('그룹B 샤피로윌크 p-value'=norm1, '그룹G 샤피로윌크 p-value'=norm2, '그룹B,그룹G 등분산성검정 p-value'=equal.var)
  return(summary)
}

group_B <- ex8_1 %>% filter(exam8_1.drug=='B') 
group_G <- ex8_1 %>% filter(exam8_1.drug=='C')
test(group_B$exam8_1.time,group_G$exam8_1.time)

## $`그룹B 샤피로윌크 p-value`
## [1] 0.9973428
## 
## $`그룹G 샤피로윌크 p-value`
## [1] 0.9132339
## 
## $`그룹B,그룹G 등분산성검정 p-value`
## [1] 0.4721646

정규성 검정은 shapiro.test를 통하여 구할 수 있다.
p-value가 정해둔 유의수준 0.05보다 크다면 유의수준 5%하에 “분포가 정규성을 따른다”는 귀무가설을 기각할 수 없다.
즉, p-value가 각각 0.997, 0.913 이므로 유의수준 0.05보다 크므로 유의수준 5%하에 두 집단 모두 정규성을 따르지 않는다고 할 충분한 증거가 없다.
등분산성 검정은 var.test (F Test to Compare Two Variances Performs an F test to compare the variances of two samples from normal populations.) 로 확인할 수 있으며 p-value가 정해둔 유의수준 0.05보다 크다면 유의수준 5%하에 “두 집단의 분산은 등분산이다”라는 귀무가설을 기각할 수 없다.
따라서 p-value가 0.472로 유의수준 0.05보다 크므로 유의수준 5%하에 “두 집단의 모분산은 등분산이 아니다”라고 할 충분한 근거가 없다.

다음은 R 내장 함수로 구한 t-value이다.

t.test(group_B$exam8_1.time,group_G$exam8_1.time,var.equal = T)

## 
##  Two Sample t-test
## 
## data:  group_B$exam8_1.time and group_G$exam8_1.time
## t = -2.4765, df = 11, p-value = 0.03076
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -1.8752609 -0.1104534
## sample estimates:
## mean of x mean of y 
##  8.750000  9.742857

직접 함수를 작성해서 구하여 보자.

two_tailed_t_test <- function(x,y){
  n1 <- length(na.omit(x))
  n2 <- length(na.omit(y))
  v1 <- n1-1
  v2 <- n2-1
  xbar1 <- mean(x)
  xbar2 <- mean(y)
  ss1 <- var(x)*v1
  ss2 <- var(y)*v2
  sp2 <- (ss1+ss2)/(v1+v2)
  s_xbar1_xbar2 <- sqrt((sp2/n1)+(sp2/n2))
  t <- (xbar1-xbar2)/s_xbar1_xbar2
  pvalue <- 2*pt(t,v1+v2)
  out <- data.frame(n1,n2,v1,v2,xbar1,xbar2=round(xbar2,2),ss1,ss2=round(ss2,4),sp2=round(sp2,4),s_xbar1_xbar2=round(s_xbar1_xbar2,2),t=round(t,3),pvalue=round(pvalue,3))
  return(out)
}

two_tailed_t_test(group_B$exam8_1.time,group_G$exam8_1.time)

##   n1 n2 v1 v2 xbar1 xbar2   ss1    ss2    sp2 s_xbar1_xbar2      t pvalue
## 1  6  7  5  6  8.75  9.74 1.695 4.0171 0.5193           0.4 -2.476  0.031

성체 수컷 토끼에게 서로 다른 약물을 투여하였을 때, 두 약물의 혈액 응고 시간에 대한 평균의 차이를 독립 이표본 t-검점을 통해 확인해 보자.
추출된 표본으로 계산한 통계량 \(\bar{X}_B=8.75 \min \ , \ \bar{X}_G=9.74 \min\)
두 표본의 등분산성을 가정하였으므로 합동분산 \(S^2_p=0.5193\)
t-값은 -2.475이고 양측 임계값은 2.201으로 좌측 임계값인 -2.201보다 t-값이 작으므로 기각역에 포함되어 귀무가설을 기각할 수 있다.
따라서 유의수준 5%하에 두 약물처리(B와G)에 따른 모든 성체 수컷토끼의 혈액 응고 시간은 다르다고 할 수 있다.

EXAMPLE 8.2

#데이터셋
ex8_2%>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
exam8_2.fertilizer	exam8_2.height
present	48.2
present	54.6
present	58.3
present	47.8
present	51.4
present	52.0
present	55.2
present	49.1
present	49.9
present	52.6
newer	52.3
newer	57.4
newer	55.6
newer	53.2
newer	61.3
newer	58.0
newer	59.8
newer	54.8

식물의 길이가 새로운 비료를 줬을 때 기존 비료를 줬을 때보다 평균이 큰지 검정하고자 한다.

\[\begin{aligned} H_0 &: \mu_1 \geq \mu_2 \\ H_A &: \mu_1 < \ \mu_2 \end{aligned}\]

기존 비료를 10개 식물에게 새로운 비료를 8개 식물에게 줬으며 기존 비료 그룹과 새로운 비료 그룹 두개의 표본은 독립적이게 추출하였다.

##정규성,등분산성 검정
test <- function(x,y) {
  norm1 = shapiro.test(x)$p.value
  norm2 = shapiro.test(y)$p.value
  equal.var = var.test(x,y)$p.value 
  summary <- list('Present Shapiro-Wilk p-value'=norm1, 'Newer Shapiro-Wilk p-value'=norm2, 'Present,Newer 등분산성검정 p-value'=equal.var)
  return(summary)
}
group_pre <- ex8_2 %>% filter(exam8_2.fertilizer=='present')
group_new <- ex8_2 %>% filter(exam8_2.fertilizer=='newer')
test(group_pre$exam8_2.height,group_new$exam8_2.height)

## $`Present Shapiro-Wilk p-value`
## [1] 0.6832982
## 
## $`Newer Shapiro-Wilk p-value`
## [1] 0.9021483
## 
## $`Present,Newer 등분산성검정 p-value`
## [1] 0.8743753

shapiro.test를 통하여 기존 비료를 준 그룹에 대한 정규성검정 p-value=0.6832이고,
새로운 비료를 준 그룹에 대한 p-value는 0.9021로 둘다 유의수준 5%하에 귀무가설을 기각할 수 없다.
즉, 유의수준 5%하에 두 집단 모두 정규성을 따르지 않는다고 할 충분한 증거가 없다.
등분산성 검정은 var.test을 통하여 p-value=0.8744로 정해둔 유의수준 0.05보다 크므로 유의수준 5%하에 “두 집단의 분산은 등분산이다”라는 귀무가설을 기각할 수 없다.
따라서 유의수준 5%하에 “두 집단의 모분산은 등분산이 아니다”라고 할 충분한 근거가 없다.

다음은 R 내장 함수로 구한 t-value이다.

t.test(group_pre$exam8_2.height,group_new$exam8_2.height,var.equal = T, alternative = "less")

## 
##  Two Sample t-test
## 
## data:  group_pre$exam8_2.height and group_new$exam8_2.height
## t = -2.9884, df = 16, p-value = 0.004343
## alternative hypothesis: true difference in means is less than 0
## 95 percent confidence interval:
##       -Inf -1.929255
## sample estimates:
## mean of x mean of y 
##     51.91     56.55

직접 함수를 작성해서 구하여 보자.

one_tailed_t_test <- function(x,y){
  n1 <- length(na.omit(x))
  n2 <- length(na.omit(y))
  v1 <- n1-1
  v2 <- n2-1
  xbar1 <- mean(x)
  xbar2 <- mean(y)
  ss1 <- var(x)*v1
  ss2 <- var(y)*v2
  sp2 <- (ss1+ss2)/(v1+v2)
  s_xbar1_xbar2 <- sqrt((sp2/n1)+(sp2/n2))
  t <- (xbar1-xbar2)/s_xbar1_xbar2
  pvalue <- pt(t,v1+v2)
  out <- data.frame(n1,n2,v1,v2,xbar1,xbar2=round(xbar2,2),ss1=round(ss1,3),ss2=round(ss2,4), s_xbar1_xbar2=round(s_xbar1_xbar2,2),t=round(t,3),pvalue=round(pvalue,4))
  return(out)
}
one_tailed_t_test(group_pre$exam8_2.height,group_new$exam8_2.height)

##   n1 n2 v1 v2 xbar1 xbar2     ss1  ss2 s_xbar1_xbar2      t pvalue
## 1 10  8  9  7 51.91 56.55 102.229 69.2          1.55 -2.988 0.0043

기존의 비료보다 새로운 비료를 사용하였을 때 식물의 평균 길이가 더 길다는 것을 검정하고자 하므로 단측검정을 시행한다.
기종 비료를 사용하였을 때 식물 길이의 표본 평균은 51.91cm이고, 새로운 비료를 사용한 식물의 길이의 표본 평균은 56.55cm이다.
합동분산 \(S^2_p=10.71cm^2\)
t-값은 -2.9935이고 단측 임계값은 1.746으로 좌측 임계값인 -1.746보다 t-값이 작으므로 기각역에 포함되어 귀무가설을 기각할 수 있다.
따라서 유의수준 5%하에 기존 비료보다 새로운 비료를 사용하였을 때 식물 길이의 모평균이 크다고 할 수 있다.

EXAMPLE 8.2a

#데이터셋
ex8_2a%>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
exam8_2a.temp	exam8_2a.days
30	40
30	38
30	32
30	37
30	39
30	41
30	35
10	36
10	45
10	32
10	52
10	59
10	41
10	48
10	55

서로 다른 실험실 온도에서 바퀴벌레 알이 부화하는 평균 시간이 다른지 검정하고자 한다.
실험실 온도에 따른 바퀴벌레 알의 부화 일수 평균에 대한 가설

\(\begin{aligned} H_0 &: \mu_{30} = \mu_{10} \\ H_A &: \mu_{30} \not=\ \mu_{10} \end{aligned}\)

30도에서 7개의 알을, 10도에서 8개의 알이 부화하는 시간을 관찰하여 기록하였고 두개의 표본은 독립적이게 추출하였다.

##정규성,등분산성 검정
test <- function(x,y) {
  norm1 = shapiro.test(x)$p.value
  norm2 = shapiro.test(y)$p.value
  equal.var = var.test(x,y)$p.value 
  summary <- list('30도 실험실 p-value'=norm1, '10도 실험실 p-value'=norm2, '30,10 등분산성검정 p-value'=equal.var)
  return(summary)
}
group_30 <- ex8_2a %>% filter(exam8_2a.temp==30)
group_10 <- ex8_2a %>% filter(exam8_2a.temp==10)

test(group_30$exam8_2a.days,group_10$exam8_2a.days)

## $`30도 실험실 p-value`
## [1] 0.7312982
## 
## $`10도 실험실 p-value`
## [1] 0.9415191
## 
## $`30,10 등분산성검정 p-value`
## [1] 0.01564653

shapiro.test를 통하여 30도 실험실 그룹에 대한 정규성검정 p-value=0.7312이고,
10도 실험실 그룹에 대한 p-value는 0.9415로 둘다 유의수준 5%하에 귀무가설을 기각할 수 없다.
즉, 유의수준 5%하에 두 집단 모두 정규성을 따르지 않는다고 할 충분한 증거가 없다.
등분산성 검정은 var.test을 통하여 p-value=0.0156으로 정해둔 유의수준 0.05보다 작으므로 유의수준 5%하에 “두 집단의 분산은 등분산이다”라는 귀무가설을 기각할 수 있다.
따라서 유의수준 5%하에 “두 집단의 모분산은 등분산이 아니다”라고 할 수 있다.

두 모집단이 정규분포를 따르지만 분산이 다른 경우는 Behrens-Fisher 검정을 이용한다.

library(asht) #Behrens-Fisher검정을 하기 위한 패키지
#sample size for t-tests with different variances and non-equal n per arm, Behrens-Fisher test, nonparametric ABC intervals, Wilcoxon-Mann-Whitney test 등등 구할 수 있다.
bfTest(group_30$exam8_2a.days,group_10$exam8_2a.days,altenative=c("two.sided"),mu=0,conf.level=0.95)

## 
##  Behrens-Fisher test
## 
## data:  x=group_30$exam8_2a.daysand y=group_10$exam8_2a.days
## t = -2.4437, R = 0.34076, p-value = 0.04436
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -16.8684039  -0.2744532
## sample estimates:
## mean of x mean of y 
##  37.42857  46.00000

30도 실험실의 바퀴벌레 알의 부화 일수 평균은 37.4days이고 10도 실험실의 바퀴벌레 알의 부화 일수 평균은 46days이다.

\[\sqrt{S^2_\bar{X_{30}}+S^2_\bar{X_{10}}}=3.51 \ days\]

t-값은 -2.44이고 양측 임계값은 2.274이다. 좌측 임계값인 -2.274보다 t-값이 작으므로 귀무가설을 기각할 수 있다.
따라서 온도가 30도인 실험실과 10도인 실험실에서 바퀴벌레 알의 부화 일수의 모평균에는 차이가 있다고 할 수 있다.
(95% 신뢰구간을 확인해 보면 (-16.87,-0.27)로 0을 포함하고 있지 않으므로 두 집단간 모평균에는 차이가 있다고 볼 수 있다.)

EXAMPLE 8.3

정밀도를 이용한 모평균차에 대한 표본크기계산
정밀도 d가 주어졌을 때 \(1-\alpha%\) 신뢰구간에 들어갈 수 있는 최소 표본 크기

\[n=\frac {2*s^2_p*t^2_{(\alpha/2,n_1+n_2-2)}}{d^2} \ _{(양측)}\] \[n=\frac {2*s^2_p*t^2_{(\alpha,n_1+n_2-2)}}{d^2} \ _{(단측)}\]

직접 함수를 작성해서 구하여 보자.

d.sample <- function(x,y, d,alpha,en,side) {
  if(sum(is.na(x)) >= 1) {
  x=na.omit(x) 
  }
  else if (sum(is.na(y)) >= 1){
    y=na.omit(y)
  } 
  else     
    {
    x=x 
    y=y
  }
  n1= length(x) 
  n2= length(y) 
  df1=n1-1
  df2= n2-1
  new_df= en-1
  x.bar1= round(mean(x),2)
  x.bar2= round(mean(y),2)
  ss1=round(sum(x^2) - ((sum(x))^2/n1), 4)
  ss2=round(sum(y^2) - ((sum(y))^2/n2),4) 
  
  sp= round((ss1 + ss2)/(df1+df2),4)
  if (side == "two"){
    ct = round(abs(qt(alpha/2,2*new_df)),3) 
  }
  else{
    ct = round(abs(qt(alpha,2*new_df)),3) 
  }
  size1= ceiling(2*sp*(ct^2) / (d^2))
  s=round((2*sp*(ct^2))/(0.5)^2,1)
  result <- list(spsquare=sp, '임계값'=ct, n=s ,sample_size=size1) 
  return(result)
}

d.sample(group_B$exam8_1.time,group_G$exam8_1.time, 0.5, 0.05, 50,'two')

## $spsquare
## [1] 0.5193
## 
## $임계값
## [1] 1.984
## 
## $n
## [1] 16.4
## 
## $sample_size
## [1] 17

정밀도 d=0.5이고 \(s^2_p=0.5193\) 표본크기를 50으로 추정하였을 때 \(t_{0.05(2),98}=1.984\)이고 표본크기는 16.4가 나온다.

d.sample(group_B$exam8_1.time,group_G$exam8_1.time, 0.5, 0.05, 17,'two')

## $spsquare
## [1] 0.5193
## 
## $임계값
## [1] 2.037
## 
## $n
## [1] 17.2
## 
## $sample_size
## [1] 18

정밀도 d=0.5이고 \(s^2_p=0.5193\) 표본크기를 17로 추정하였을 때 \(t_{0.05(2),32}=2.037\)이고 표본크기는 17.2가 나온다.

d.sample(group_B$exam8_1.time,group_G$exam8_1.time, 0.5, 0.05, 18,'two')

## $spsquare
## [1] 0.5193
## 
## $임계값
## [1] 2.032
## 
## $n
## [1] 17.2
## 
## $sample_size
## [1] 18

정밀도 d=0.5이고 \(s^2_p=0.5193\) 표본크기를 18로 추정하였을 때 \(t_{0.05(2),98}=2.032\)이고 표본크기는 17.2가 나온다.

표본크기를 18로 추정하였을 때가 주어진 정밀도에 가장 밀접하다.
여기서 n은 요구되는 그룹별 표본크기이다.
따라서 그룹B, 그룹G 각각 18개의 표본크기를 가져야 한다.

두 그룹에 대한 표본 할당비가 다른 경우 표본크기 계산법

\[n=\frac{k}{\frac{1}{n_1}\ldots\frac{1}{n_k}} \ ,\ _{k는} \ _{그룹수}\]

조화 평균을 이용해서 계산한다.
그룹1의 표본크기\(n_1\)를 고정시키고 그룹 2의 표본크기\(n_2\)를 구하는 경우 (위 식과 동일)

\[n_2 = \frac{nn_1}{2n_1-n}\]

예를 들어 \(n(그룹별 표본크기)=18, \ n_1=14\)인 경우

n=18
n1=14
n2=n*n1 / (2*n1-n)
n2

## [1] 25.2

\(n_2\)=25.2 , 약 26이다.

최소 요구되는 총 표본크기는 14+26=40

EXAMPLE 8.4

\[\begin{aligned} n &\ge \frac{2s_p^2}{\delta^2}(t_{(\frac{\alpha}{2},n_1+n_2-2)}+t_{(\beta,n_1+n_2-2)})^2 \ _{(양측)} \end{aligned}\] \[\begin{aligned} n &\ge \frac{2s_p^2}{\delta^2}(t_{(\alpha,n_1+n_2-2)}+t_{(\beta,n_1+n_2-2)})^2 \ _{(단측)} \end{aligned}\]

표본 크기가 100일 때,자유도=100+100-2=198이고 이에 대응되는 임계값

t_alpha <- round(qt(0.025, 198,lower.tail = F),3) 
t_beta <- round(qt(0.10,198,lower.tail = F), 3)

t_alpha

## [1] 1.972

\[t_{0.05(2),198}=1.972\]

t_beta

## [1] 1.286

\[t_{0.10(1),198}=1.286\]

bound <- round(2*0.52 / 0.5^2 *(t_alpha+t_beta)^2, 1)
bound

## [1] 44.2

\[n \ge 44.2\]

표본 크기가 45일 때,자유도=45+45-2=88이고 이에 대응되는 임계값

t_alpha <- round(qt(0.025, 88,lower.tail = F),3)
t_beta <- round(qt(0.10,88,lower.tail = F), 3)

t_alpha

## [1] 1.987

\[t_{0.05(2),88}=1.987\]

t_beta

## [1] 1.291

\[t_{0.10(1),88}=1.291\]

bound <- round(2*0.52 / 0.5^2 *(t_alpha+t_beta)^2, 1)
bound

## [1] 44.7

\[n \ge 44.7\]

따라서 두 표본의 크기는 각각 최소한 45 이상이여야 한다.
그룹1의 표본크기\(n_1\)=30으로 고정시키고 그룹 2의 표본크기\(n_2\)를 구하는 경우

n=44.7
n1=30
n2=n*n1 / (2*n1-n)
n2

## [1] 87.64706

n(그룹별 표본 크기)은 위에서 구한 44.7로 두고 \(n_1\)=30으로 고정되어 있을 때 \(n_2\)는 88이다.

EXAMPLE 8.5

최소 검출차 (minimum detectable difference:MDD)

\[\delta \ge \sqrt{\frac{2s_p^2}{n}}t_{(\frac{\alpha}{2},n_1+n_2-2)}+t_{(\beta,n_1+n_2-2)} \ _{(양측)}\] \[\delta \ge \sqrt{\frac{2s_p^2}{n}}t_{(\alpha,n_1+n_2-2)}+t_{(\beta,n_1+n_2-2)} \ _{(단측)}\]

delta <- sqrt(2*0.5193 / 20)*(qt(0.025,38,lower.tail = F) + qt(0.1,38,lower.tail = F))
round(delta, 2)

## [1] 0.76

\(n\)(표본 크기)=20, \(\alpha\)=0.05, \(\beta\)=1-0.9=0.1로 주어졌을 때 검출 가능한 최소 차이는 0.76min이다.

EXAMPLE 8.6

Example 8.1에 대하여 \(n_1=n_2=15\), and \(\alpha(2)=0.05\)하에 두 약물을 사용하여 사람의 평균 혈액 응고 시간 간에 1분의 차이를 검출할 확률
검정력 공식

\[\ t_{(\beta,n_1+n_2-2)} \leq \frac{\delta}{\sqrt{\frac{2s^2_p}{n}}} \ -t_{(\frac{\alpha}{2},n_1+n_2-2)} \ _{(양측)}\] \[\ t_{(\beta,n_1+n_2-2)} \leq \frac{\delta}{\sqrt{\frac{2s^2_p}{n}}} \ -t_{(\alpha,n_1+n_2-2)} \ _{(단측)}\]

delta <- 1
n <- 15
sp <- 0.5193
t_alpha<- 2.048
t_beta <- delta/(sqrt((2*sp)/15))-t_alpha
round(t_beta,3)

## [1] 1.752

\[\ t_{(\beta(1),28)} \leq 1.752\]

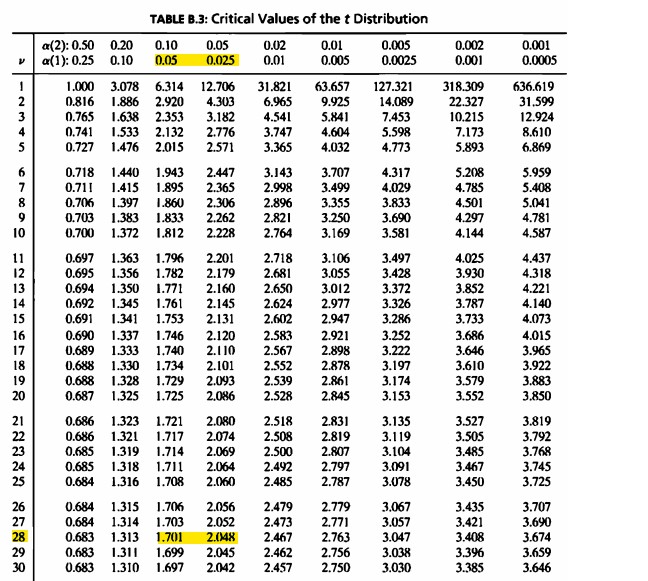
\(P(t\geq1.752)\) (단측) 자유도=28인 확률은 (0.025,0.05)구간에 있다. 따라서 \(0.025<\beta<0.05\)

\[Power=1-\beta, \ so \ 0.95<power<0.975\]

표준정규분포 근사 값으로 구한 정규분포 확률은 \(\beta \ by \ P(Z\geq1.752)=0.04\)이다. 따라서 power=0.96이다.

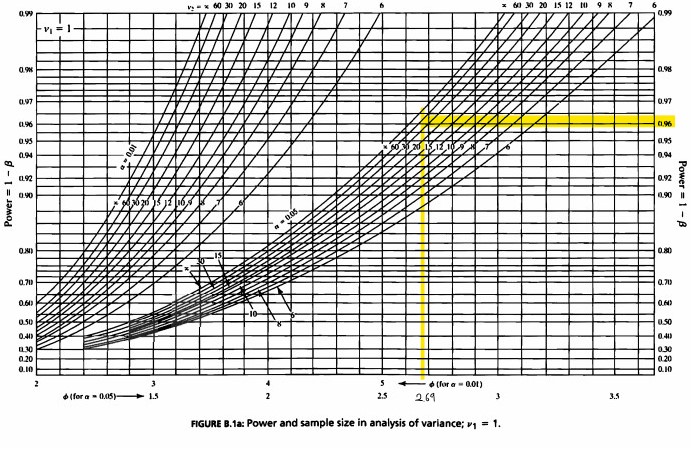
\[\phi=\sqrt{(\frac{n\delta^2}{4s^2_p})}=\sqrt{(\frac{15(1.0)^2}{4(0.5193)})}=2.69\]

표를 참고하여 보면 \(\phi=2.69 \ and \ \nu(=\nu_2)=28\)은 약 0.96의 검정력과 관련이 있게 나온다.

EXAMPLE 8.7

type1,type2인 trap에 따라 잡히는 나방의 수의 표본을 구했다.
trap 종류에 따라 잡힌 나방의 수에 대한 분산의 비가 다른가에 대한 검정으로 모집단의 분산 차이가 있는지 알아보고자 한다.

\[\ H_0:\sigma^2_1 = \sigma^2_2 \ vs \ H_A: \sigma^2_1 \not= \sigma^2_2\]

##정규성,등분산성 검정
test <- function(x,y) {
  norm1 = shapiro.test(x)$p.value
  norm2 = shapiro.test(y)$p.value
  summary <- list('type1 샤피로윌크 p-value'=norm1, 'type2 샤피로윌크 p-value'=norm2)
  return(summary)
}
group_1 <- ex8_7 %>% filter(exam8_7.trap==1)
group_2 <- ex8_7 %>%  filter(exam8_7.trap==2)

test(group_1$exam8_7.number,group_2$exam8_7.number)

## $`type1 샤피로윌크 p-value`
## [1] 0.8921986
## 
## $`type2 샤피로윌크 p-value`
## [1] 0.9156178

분산비를 검정하기 전에 각 모집단의 표본이 정규성을 따르는지 shapiro-wilk test로 검정하였다.
shapiro-wilk p-value가 각각 0.892, 0.916 이므로 유의수준 0.05보다 크므로 유의수준 5%하에 두 집단 모두 정규성을 따르지 않는다고 할 충분한 증거가 없다.

n1 <- length(group_1$exam8_7.number) 
n2 <- length(group_2$exam8_7.number)
var1 <- round(var(group_1$exam8_7.number), 2)
var2 <- round(var(group_2$exam8_7.number), 2)
F_stat <- round(var1 / var2, 2)
list(n1=n1, n2=n2, var1=var1, var2=var2,"F"=F_stat)

## $n1
## [1] 11
## 
## $n2
## [1] 10
## 
## $var1
## [1] 21.87
## 
## $var2
## [1] 12.9
## 
## $F
## [1] 1.7

각 표본의 크기와 분산이 구해졌고 분산비 F=1.70으로 나왔다.

\(F_{0.05(2),10,9}\)=3.96 이다. F-값=1.7이 임계값(3.96)보다 작으므로 기각역에 포함되지 않고 따라서 귀무가설을 기각할 만한 충분한 근거가 없다.
또한 p-value를 확인 하여도 유의수준 5%보다 크므로 유의수준 5%하에 유의하다고 볼 수 없다.
즉, trap의 종류에 따라 잡힌 나방의 수의 모분산이 같지 않다고 할 수 없다.

EXAMPLE 8.8

#데이터셋
ex8_8%>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
exam8_8.site	exam8_8.time
1	69.3
1	75.5
1	81.0
1	74.7
1	72.3
1	78.7
1	76.4
2	69.5
2	64.6
2	74.0
2	84.8
2	76.0
2	93.9
2	81.2
2	73.4
2	88.0

Greenhouse,Outside에서 소나무 종자 발아 시간을 각각 측정하였다.
두 상황에서 추출한 두 데이터로 Outside에서의 소나무 종자 발아 시간의 모분산이 Greenhouse에서 보다 모분산이 더 큰지 검정하고자 한다.

\[\ H_0:\sigma^2_1 \geq \sigma^2_2 \ vs \ H_A: \sigma^2_1 < \sigma^2_2\]

##정규성,등분산성 검정
test <- function(x,y) {
  norm1 = shapiro.test(x)$p.value
  norm2 = shapiro.test(y)$p.value
  summary <- list('Greenhouse 샤피로윌크 p-value'=norm1, 'Outside 샤피로윌크 p-value'=norm2)
  return(summary)
}
group_G <- ex8_8 %>% filter(exam8_8.site==1)
group_O <- ex8_8 %>% filter(exam8_8.site==2)

test(group_G$exam8_8.time,group_O$exam8_8.time)

## $`Greenhouse 샤피로윌크 p-value`
## [1] 0.993425
## 
## $`Outside 샤피로윌크 p-value`
## [1] 0.9566238

분산비를 검정하기 전에 각 모집단의 표본이 정규성을 따르는지 shapiro-wilk test로 검정하였다.
shapiro-wilk p-value가 각각 0.993, 0.956 이므로 유의수준 0.05보다 크므로 유의수준 5%하에 두 집단 모두 정규성을 따르지 않는다고 할 충분한 증거가 없다.

n1 <- length(group_G$exam8_8.time) 
n2 <- length(group_O$exam8_8.time)
var1 <- round(var(group_G$exam8_8.time), 2)
var2 <- round(var(group_O$exam8_8.time), 2)
F_stat <- round(var2 / var1, 2)
list(n1=n1, n2=n2, var1=var1, var2=var2,"F"=F_stat)

## $n1
## [1] 7
## 
## $n2
## [1] 9
## 
## $var1
## [1] 15.09
## 
## $var2
## [1] 87.62
## 
## $F
## [1] 5.81

각각의 분산은 \(s^2_1=15.10\), \(s^2_2=87.62\)이고, \(F=\frac{s^2_1}{s^2_2} \ or \ F=\frac{s^2_2}{s^2_1}\) 둘 중 큰 값을 사용한다.
따라서 \(F=\frac{s^2_2}{s^2_1}= \frac{87.62}{15.10}=5.80\)이다.
F-값이 임계값 \(F_{0.05(1),8,6}=4.15\) 보다 크므로 기각역에 포함되고 귀무가설을 기각할 수 있다.
따라서 Greenhouse에서 소나무 종자 발아 시간 모분산은 Outside에서 소나무 종자 발아 시간 모분산 보다 작다고 할 수 있다.

EXAMPLE 8.9

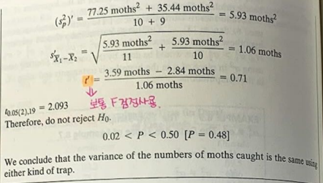
library(lawstat) #levene test를 위한 패키지
levene.test(ex8_7$exam8_7.number,ex8_7$exam8_7.trap,location='mean')

## 
##  Classical Levene's test based on the absolute deviations from the mean
##  ( none not applied because the location is not set to median )
## 
## data:  ex8_7$exam8_7.number
## Test Statistic = 0.49267, p-value = 0.4913

Levene test를 통하여 분산의 동일성 검정을 할 수 있다.
Levene test는 모집단이 정규분포를 따르지 않는 경우에 모분산의 동질성을 검정하기 위하여 사용한다.
p-value = 0.4913으로 출력된 것을 볼 수 있다. 그러므로 유의수준 5%하에서 귀무가설을 기각할 충분한 근거가 없다.

두 종류의 trap에 따라 잡히는 나방의 수의 모분산이 같지 않다는 증거가 충분하지 않다고 할 수 있다.

EXAMPLE 8.10

#데이터셋
ex8_10%>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
exam8_10.weight	exam8_10.height
72.5	183.0
71.7	172.3
60.8	180.1
63.2	190.2
71.4	191.4
73.1	169.6
77.9	166.4
75.7	177.6
72.0	184.7
69.0	187.5
NA	179.8

같은 모집단에서 추출된 남성의 키와 몸무게의 변동이 다른지를 검정하고자 한다.
키의 측정 단위는 cm이고, 몸무게의 측정단위는 kg이다.
단위가 다른 두 데이터의 비교를 위해 변동계수 (coefficients of variantion)을 산출하여 비교하였다.
따라서 가설은 다음과 같이 설정할 수 있다.

\[\begin{aligned} H_0 &:\frac{\sigma_1}{\mu_1}=\frac{\sigma_2}{\mu_2}, \\ H_A &:\frac{\sigma_1}{\mu_1} \neq \frac{\sigma_2}{\mu_2} \end{aligned}\]

##정규성,등분산성 검정
test <- function(x,y) {
  norm1 = shapiro.test(x)$p.value
  norm2 = shapiro.test(y)$p.value
  summary <- list('weight 샤피로윌크 p-value'=norm1, 'height 샤피로윌크 p-value'=norm2)
  return(summary)
}

test(ex8_10$exam8_10.weight,ex8_10$exam8_10.height)

## $`weight 샤피로윌크 p-value`
## [1] 0.2660832
## 
## $`height 샤피로윌크 p-value`
## [1] 0.7483809

p-value가 각각 \(p\ value=0.2661,\ 0.7484\) 으로 유의수준 0.05보다 크기에 귀무가설 \(H_0\) 를 기각할만한 충분한 근거가 없다. 데이터셋이 정규성을 따르지 않는다는 충분한 근거가 없기에 분산 비의 검정을 수행할 수 있다.

분산비 검정을 하기 위하여 통계량 구하는 함수를 작성하여 보자.

library(kableExtra)
f8_10 <- function(x,y){
  x <- na.omit(x)
  y <- na.omit(y)
  n1 <- length(x)
  n2 <- length(y)
  v1 <- n1-1
  v2 <- n2-1
  xbar1 <- mean(x)
  xbar2 <- mean(y)
  s1 <-var(x)
  s2 <- var(y)
  ss1 <- var(x)*v1
  ss2 <- var(y)*v2
  sd1 <- sd(x)
  sd2 <- sd(y)
  cv1 <- sd1/xbar1
  cv2 <- sd2/xbar2
  sslog1 <- var(log10(x))*v1
  sslog2 <- var(log10(y))*v2
  slog1 <- var(log10(x))
  slog2 <- var(log10(y))
  if(slog1 > slog2){
    f <- slog1/slog2
  }
  else{
    f <- slog2/slog1
  }
  pvalue <- 2*(1-pf(f,max(v1,v2),min(v1,v2)))
  if(pvalue < 0.05){
    Reject_H0 <- "yes"
    sp2 <- NA
  }
  else{
    Reject_H0 <- "No"
  }
  out1 <- c(n=n1,v=v1,xbar=round(xbar1,2), s_2=round(s1,4),s=round(ss1,4),CV =round(cv1,4),SSlog=round(sslog1,8),s_2log=round(slog1,8),F=round(f,2),
            pvalue=round(pvalue,2),Reject_H0)
  out2 <- c(n=n2,v=v2,xbar=round(xbar2,2), s_2=round(s2,4),s=round(ss2,4),CV =round(cv2,4),SSlog=round(sslog2,8),s_2log=round(slog2,8),F=round(f,2),
            pvalue=round(pvalue,2),Reject_H0)
  out <-as.data.frame(cbind(out1,out2))
  names(out) <- c("Weight","Height")
  rownames(out)[11] <- "Reject_H0"
  return(out)
}

f8_10(ex8_10$exam8_10.weight,ex8_10$exam8_10.height) %>%
  kbl(caption = "Result of Variance ratio test") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Result of Variance ratio test
	Weight	Height
n	10	11
v	9	10
xbar	70.73	180.24
s_2	27.3512	67.8945
s	246.161	678.9455
CV	0.0739	0.0457
SSlog	0.00986951	0.00400214
s_2log	0.00109661	0.00040021
F	2.74	2.74
pvalue	0.14	0.14
Reject_H0	No	No

몸무게의 CV=0.0739, 키의 CV=0.0457
Lewontin은 data를 logarithmic transformation하여 변동계수 검정을 수행하는 방법을 증명하였다.
각 표본의 data들에 log10 변환을 하여 산출한 분산은 몸무게=0.0010967, 키=0.00040019이고,
이를 활용한 F-value는 \(F=\frac{0.0010967}{0.00040019}=2.74\)이다.
임계값보다 F-value가 작으므로 귀무가설을 기각할 수 없다.

즉, 같은 모집단으로부터 추출된 남성의 키와 몸무게의 변동은 다르다고 할 증거가 충분하지 못하다.

cv1 <- as.numeric(f8_10(ex8_10$exam8_10.weight,ex8_10$exam8_10.height)$Weight[6])
cv2 <- as.numeric(f8_10(ex8_10$exam8_10.weight,ex8_10$exam8_10.height)$Height[6])
v1 <- as.numeric(f8_10(ex8_10$exam8_10.weight,ex8_10$exam8_10.height)$Weight[2])
v2 <- as.numeric(f8_10(ex8_10$exam8_10.weight,ex8_10$exam8_10.height)$Height[2])
vp <- (v1*cv1+v2*cv2)/(v1+v2)
vp2 <- round(vp,4)^2
Z <- (cv1-cv2)/sqrt(((vp2/v1)+(vp2/v2))*(0.5+vp2))
pvalue <- 2*(1-pt(Z,v1+v2))

if(pvalue < 0.05){
  Reject_H0 <- "yes"
}else{
  Reject_H0 <- "No"
}

ztest <- data.frame(vp=round(vp,4),vp2=round(vp2,6),Z=round(Z,2),pvalue=round(pvalue,2),Reject_H0)
ztest%>%
  kbl(caption = "Result of Z test") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Result of Z test
vp	vp2	Z	pvalue	Reject_H0
0.0591	0.003493	1.46	0.16	No

Miller는 공통 변동계수를 산출하여 Z분포를 활용해 변동계수 차에 대한 가설 검정을 수행하였다.
공통 변동계수는 \(V_p=\frac{\nu_1V1+\nu_2V2}{\nu_1+\nu_2}=\frac{9(0.0739)+10(0.0457)}{9+10}=0.0591\)이다.
공통 변동계수를 활용한 Z-value=1.46이고, 유의수준 5%하에서 임계값 z=1.96이다.
z-value가 임계값 보다 작으므로, 기각역에 포함되지 않아 귀무가설을 기각할 수 없다.

즉, 같은 모집단으로부터 추출된 남성 키와 몸무게의 변동은 다르다고 하기 어렵다.

EXAMPLE 8.11

#데이터셋
ex8_11%>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
exam8_11.sex	exam8_11.height
1	193
1	188
1	185
1	183
1	180
1	175
1	170
2	178
2	173
2	168
2	165
2	163

본 데이터는 성인 남성과 여성의 키를 기록한 데이터이다.
데이터를 그룹별로 나누어 보자.

hm <- ex8_11 %>% filter(exam8_11.sex=='1') 
hf <- ex8_11 %>% filter(exam8_11.sex=='2')

library(qpcR) # 결측치 있는 데이터 cbind   
ex8_11_cbind<- data.frame(qpcR:::cbind.na(hm[,2], hf[,2]))
names(ex8_11_cbind) <- c("Heights of males","Heights of females")

males와 females 데이터 수가 차이나기 때문에 cbind가 되지 않으므로 qpcR패키지를 사용하여 결합시켜준다.

ex8_11_cbind%>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
Heights of males	Heights of females
193	178
188	173
185	168
183	165
180	163
175	NA
170	NA

남학생과 여학생 키의 차이에 대한 검정을 하고자 한다.
일반적인 t-검정을 수행하기엔 표본의 수가 적어 비모수 검정 방법인 Mann-Whitney검정을 실시한다.

\[\begin{aligned} H_0 &: \ Male \ and \ female \ students\ are\ the\ same\ height.\\ H_A &:\ Male\ and\ female\ students\ are\ not\ the\ same\ height. \end{aligned}\]

Mann-Whitney 검정을 하기 위해서는 각 변수의 랭크(순위)를 매겨야하기 때문에 이를 구하도록 한다.
(이 예제의 경우 내림차순으로 순위를 구했다. 양측일 경우 문제 없지만 단측일 경우 통계량 값이 바뀐다.)

rank8_11 <- function(data){
  x <- data[,1]
  y <- data[,2]
  h <- as.numeric(rbind(c(x,y)))
  rank <- rank(-h, na.last = "keep")
  gender <- c(rep("m",length(x)),rep("f",length(y)))
  out <- data.frame(h,rank,gender)
  data$rank_m <- subset(out$rank, gender=="m")
  data$rank_f <- subset(out$rank, gender=="f")
  return(data)
}

dat8_11 <- rank8_11(data=ex8_11_cbind)

dat8_11%>%
  kbl(caption = "Result of Rank") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Result of Rank
Heights of males	Heights of females	rank_m	rank_f
193	178	1	6
188	173	2	8
185	168	3	10
183	165	4	11
180	163	5	12
175	NA	7	NA
170	NA	9	NA

Mann-Whitney 검정통계량을 구하는 공식은 다음과 같다.

\[U=n_1n_2 + \frac{n_1(n_1+1)}{2}-R_1\]

\(U'=n_2n_1 + \frac{n_2(n_2+1)}{2}-R_2\)

\(U'\)을 쉽게 구하는 방법이 있다.

\[U'=n_1n_2-U\]

본 검정에서 임계값을 테이블을 통해확인하여 보자.

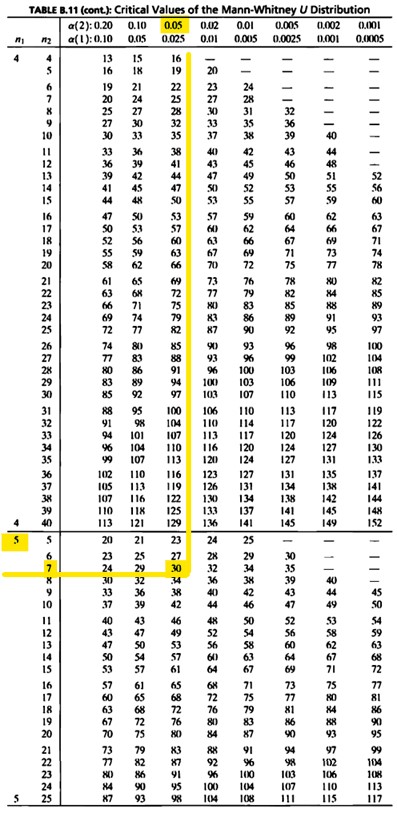
양측 0.05 n=5,7의 임계값은 30인 것을 볼 수 있다.

M_W_test <- function(x,y,a,b){
  x <- na.omit(x)
  y <- na.omit(y)
  a <- na.omit(a)
  b <- na.omit(b)
  n1 <- length(x)
  n2 <- length(y)
  r1 <- sum(a) 
  r2 <- sum(b) 
  u <- n1*n2+(n1*(n1+1)/2)-r1
  u_prime <- n1*n2-u
  out <- data.frame(n1,n2,R1=r1,R2=r2,U=u,U_prime=u_prime)
  return(out)
}

M_W_test(dat8_11$`Heights of males`,dat8_11$`Heights of females`,dat8_11$rank_m,dat8_11$rank_f) %>%
  kbl(caption = "Result of Mann-Whitney test") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Result of Mann-Whitney test
n1	n2	R1	R2	U	U_prime
7	5	31	47	32	3

\[U=7*5+\frac{7(7+1)}{2}-31=32\] \[U'=7*5-32=3\]

이 검정은 양측검정이기 때문에 \(U, \ U'\) 중 하나가 임계값보다 크거나 같으면 귀무가설을 기각한다.
임계값 U는 30으로 나왔고, 임계값보다 산출된 \(U\) 통계량 32가 더 크므로 유의수준 5%하에 귀무가설을 기각할 수 있다.

즉, 남학생과 여학생의 키는 유의수준 5%하에서 다르다고 할 수 있다.

다음은 R에 내장된 wilcox.text() 를 사용한 결과를 확인하여 보자.

wilcox.test(dat8_11$`Heights of males`, dat8_11$`Heights of females`)

## 
##  Wilcoxon rank sum exact test
## 
## data:  dat8_11$`Heights of males` and dat8_11$`Heights of females`
## W = 32, p-value = 0.01768
## alternative hypothesis: true location shift is not equal to 0

wilcoxon rank sum exact test의 p-value=0.018로 유의수준 5%하에서 귀무가설을 기각할 수 있다.
그러므로 남학생과 여학생의 키는 다르다고 할 수 있다.

EXAMPLE 8.12

#데이터셋
wt <- c(44,48,36,32,51,45,54,56)
wot <- c(32,40,44,44,34,30,26,NA)
ex8_12 <- data.frame(wt,wot)
ex8_12%>%
  kbl(caption = "Dataset",escape=F) %>%
   kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
wt	wot
44	32
48	40
36	44
32	44
51	34
45	30
54	26
56	NA

고등학교에서 typing 훈련을 받은 대학생이 훈련을 받지 않은 사람보다 평균속도가 좋은지 검정하고자 한다.

\[\begin{aligned} H_0 &: Typing\ speed\ is\ not\ greater\ in\ college\ students\ having\ had\ high\ school\ typing\ training. \\ H_A &: Typing\ speed\ is\ greater\ in\ college\ students\ having\ had\ high\ school\ typing\ training. \end{aligned}\]

Mann-Whitney 검정을 하기 위해서는 각 변수의 랭크(순위)를 매겨야하기 때문에 이를 구하도록 한다.
(이 예제의 경우 오름차순으로 순위를 구했다.)
동률 순위 자료가 있는 경우 동률 순위의 평균 순위를 이용한다.

rank8_12 <- function(data){
  x <- data[,1]
  y <- data[,2]
  h <- as.numeric(rbind(c(x,y)))
  rank <- rank(h, na.last = "keep")
  gender <- c(rep("m",length(x)),rep("f",length(y)))
  out <- data.frame(h,rank,gender)
  data$rank_m <- subset(out$rank, gender=="m")
  data$rank_f <- subset(out$rank, gender=="f")
  return(data)
}
dat8_12 <- rank8_12(data=ex8_12)

dat8_12%>%
  kbl(caption = "Result of Rank") %>%
   kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Result of Rank
wt	wot	rank_m	rank_f
44	32	9.0	3.5
48	40	12.0	7.0
36	44	6.0	9.0
32	44	3.5	9.0
51	34	13.0	5.0
45	30	11.0	2.0
54	26	14.0	1.0
56	NA	15.0	NA

이제 Mann-Whitney 검정통계량을 구해 검정을 실시하도록 한다.

M_W_test(dat8_12$wt,dat8_12$wot,dat8_12$rank_m,dat8_12$rank_f) %>%
  kbl(caption = "Result of Mann-Whitney test") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Result of Mann-Whitney test
n1	n2	R1	R2	U	U_prime
8	7	83.5	36.5	8.5	47.5

\[U=8*7+\frac{8(8+1)}{2}-83.5=8.5\] \[U'=8*7-8.5=47.5\]

본 검정에서 임계값을 테이블을 통해확인하여 보자.

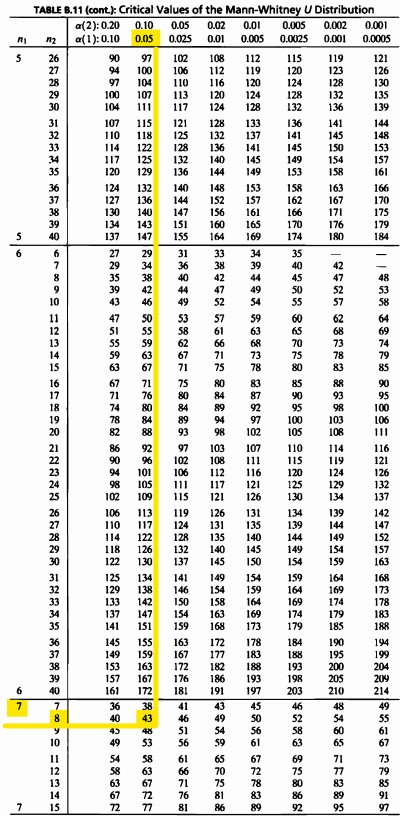
단측 0.05 n=7,8의 임계값은 43인 것을 볼 수 있다.
이 검정은 단측검정이기 때문에 다음의 표를 확인하여야 한다.

이 예제는 오름차순으로 순위가 매겨져 있으며, 훈련받은 학생의 평균속도가 더 좋은지 검정하는 것이기 때문에 통계량을 \(U'\)을 사용한다.
임계값은 43으로 나왔고, 임계값보다 산출된 \(U'\) 통계량 47.5가 더 크므로 유의수준 5%하에 귀무가설을 기각할 수 있다.

즉, 고등학교에서 typing 훈련을 받은 학생은 훈련을 받지 않은 학생보다 typing 평균 속도가 빠르다고 할 수 있다.

다음은 R에 내장된 wilcox.text() 를 사용한 결과를 확인하여 보자.

wilcox.test(dat8_12$wt,na.omit(dat8_12$wot),alternative = "greater")

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  dat8_12$wt and na.omit(dat8_12$wot)
## W = 47.5, p-value = 0.0136
## alternative hypothesis: true location shift is greater than 0

wilcoxon rank sum exact test의 p-value=0.0136으로 유의수준 5%하에서 귀무가설을 기각할 수 있다.
그러므로 고등학교에서 typing 훈련을 받은 학생은 훈련을 받지 않은 학생보다 typing 평균 속도가 빠르다고 할 수 있다.

EXAMPLE 8.13

본 데이터는 보충제를 섭취 유무에 따른 동물들의 체중을 기록한 데이터로 단측 검정에서의 Mann-Whitney 검정을 실시할 때의 정규 근사를 보여주는 예시이다.
Mann-Whitney 검정에서 두 그룹의 표본이 20 이상이고 두 표본의 크기 합이 40이상일 경우 정규 근사가 가능하다.
각 표본의 sample sizw는 20을 넘어 Mann-Whitney의 정규근사를 이용하여 검정을 수행하였다.

\[\begin{aligned} H_0 &: Body\ weight\ of\ animals\ on\ the\ supplemented\ diet\ are\ not\ greater\ than\ those\ on\ the\ unsupplemented\ diet. \\ H_A &: Body\ weight\ of\ animals\ on\ the\ supplemented\ diet\ are\ greater\ than\ those\ on\ the\ unsupplemented\ diet. \end{aligned}\]

Mann-Whitney의 정규근사를 위한 통계량

\[\mu_U=\frac{n_1n_2}{2} \ (=\frac{U+U'}{2}), \ \sigma_U=\sqrt{\frac{n_1n_1(N+1)}{12}}\]

\(\rightarrow \space Z= \frac{U-\mu_U}{\sigma_U}\ \sim\ N(0,1)\)

\(n_1=22,\ n_2=46,\ N=68,\ U=282\) 가 주어졌을 때 검정을 해보도록 한다.

Normal_Approximation_M_W_test<-function(n1,n2,u){
  u_prime<-(n1*n2)-u
  mu<-(n1*n2)/2
  sig<-sqrt(((n1*n2)*(n1+n2+1))/12)
  z<-(u_prime -mu)/sig
  pvalue <- 1-pnorm(z)
  if(pvalue < 0.05){
    Reject_H0 <- "yes"
  }else{
    Reject_H0 <- "No"
  }
  out <- data.frame(u_prime,mu,sig=round(sig,2),z=round(z,2),p_value=round(pvalue,4),Reject_H0)
  return(out)
}

Normal_Approximation_M_W_test(22,46,282) %>%
  kbl(caption = "Result of Mann-Whitney test (Normal approxiation)") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Result of Mann-Whitney test (Normal approxiation)
u_prime	mu	sig	z	p_value	Reject_H0
730	506	76.28	2.94	0.0017	yes

이 예제는 오름차순으로 순위가 매겨져 있으며, 음식 보충제를 섭취한 동물의 체중이 음식 보충제를 섭취하지 않은 동물의 체중보다 큰지 검정하는 것이기 때문에 통계량을 \(U'\)을 사용한다.
산출된 통계량을 이용하여 \(Z=\frac{U'-\mu_U}{\sigma_U}=2.94\)이고, 표준정규분포에서 유의수준 5% 단측검정 임계값은 1.6449이다.
계산된 통계량 값이 임계값 보다 크고, 기각역에 포함되므로 귀무가설을 기각할 수 있다.
따라서 음식 보충제를 섭취한 동물의 체중은 음식 보충제를 섭취하지 않은 동물의 체중보다 많이 나간다고 말할 수 있다.

EXAMPLE 8.14

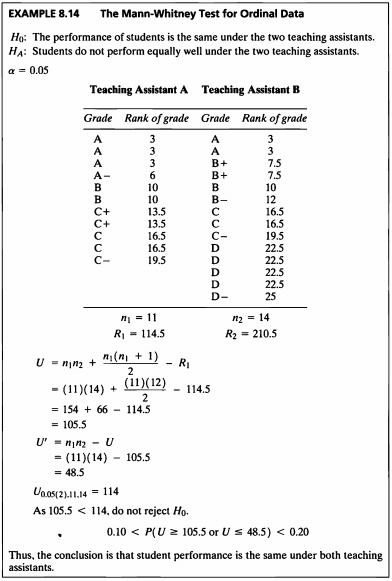
연속형 데이터가 아닌 순서(순위)만 있는 데이터의 검정을 해보도록 한다.
본 데이터는 수업 조교에 따른 학생들의 성적 등급을 기록한 데이터로 수업 조교에 따른 학생들의 등급이 같은지 다른지 검정해보도록 한다.

A <- c(3,3,3,6,10,10,13.5,13.5,16.5,16.5,19.5,NA,NA,NA)
B <- c(3,3,7.5,7.5,10,12,16.5,16.5,19.5,22.5,22.5,22.5,22.5,25)
ex8_14 <- data.frame(A,B)
ex8_14%>%
  kbl(caption = "Dataset",escape=F) %>%
   kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
A	B
3.0	3.0
3.0	3.0
3.0	7.5
6.0	7.5
10.0	10.0
10.0	12.0
13.5	16.5
13.5	16.5
16.5	19.5
16.5	22.5
19.5	22.5
NA	22.5
NA	22.5
NA	25.0

rank_M_W_test <- function(x,y){
  x <- na.omit(x)
  y <- na.omit(y)
  n1 <- length(x)
  n2 <- length(y)
  r1 <- sum(x) 
  r2 <- sum(y) 
  u <- n1*n2+(n1*(n1+1)/2)-min(r1,r2)
  u_prime <- n1*n2-u
  out <- data.frame(n1,n2,R1=r1,R2=r2,U=u,U_prime=u_prime)
  return(out)
}

rank_M_W_test(ex8_14$A,ex8_14$B)%>%
  kbl(caption = "Result of Mann-Whitney test (Normal approxiation)") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Result of Mann-Whitney test (Normal approxiation)
n1	n2	R1	R2	U	U_prime
11	14	114.5	210.5	105.5	48.5

\(U\) 통계량은 주어진 공식에 따라 \(U, U'\)을 모두 구하고 둘 중 큰 값을 \(U\) 통계량으로 한다.**
계산 결과 \(U=105.5, \ U'=48.5\)로 \(U\)값이 더 크기 때문에 통계량은 105.5가 된다.

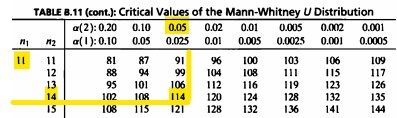
임계값은 U_0.05(11,14)=114이므로 통계량이 임계값보다 작아 귀무가설을 기각할 수 없고 따라서 어시스턴트에 따라 학생들의 학업 성취도가 다르다고 말할 수 없다.**

다음은 R에 내장된 wilcox.text() 를 사용한 결과이다.

wilcox.test(na.omit(ex8_14$A),ex8_14$B,alternative = "two.sided")

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  na.omit(ex8_14$A) and ex8_14$B
## W = 48.5, p-value = 0.1219
## alternative hypothesis: true location shift is not equal to 0

wil.cox test를 이용해 검정할 수도 있으며 패키지를 이용해 wilcox.test검정을 진행한 결과 p-value가 0.1219로 유의수준 0.05보다 크기 때문에 귀무가설을 기각할 수 없다.

EXAMPLE 8.15

Example 8.14 데이터를 사용해서 중위수 검정을 실시해보도록 한다.

\[\begin{aligned} H_0 &: The\ median\ performance\ is\ the\ same\ under\ the\ two\ teaching\ assistants.\\ H_A &: The\ median\ of\ the\ two\ sampled\ populations\ are\ not\ equal. \end{aligned}\]

data <- c(na.omit(ex8_14$A),ex8_14$B)
ex8_15 <- data.frame(data)
ex8_15$number <- ifelse(ex8_15$data > median(ex8_15$data) ,
                         ex8_15$number <- "Not above Median",ifelse(ex8_15$data == median(ex8_15$data),NA,ex8_15$number <- "Above Median"))
group<-c(rep("Sample 1",11), rep("Sample 2",14))
ex8_15$group <- group
ex8_15 <- na.omit(ex8_15)
table(ex8_15$number,ex8_15$group)%>%
  kbl(caption = "Result of Mann-Whitney test") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive")) 

Result of Mann-Whitney test
	Sample 1	Sample 2
Above Median	6	6
Not above Median	3	8

교차표를 보면 1번 그룹에선 중위수를 넘는 학생이 6명이고 넘지 않는 학생이 3명이며, 2번 그룹에서는 6명과 8명이다.
중위수 검정을 하기 위해 pearson 카이제곱 검정을 실시한다. 카이제곱 검정을 하기 위한 검정통계량 공식은 다음과 같다.

\[\chi_c^2 = \frac{n\ (|f_{11}f_{22}\ -\ f_{12}f_{21}|\ -\ \frac{n}{2})^2}{(C_1)(C_2)(R_1)(R_2)} \ \sim \chi_1^2\]

chi_square_test<- function(table){
  tab <- table
  f11 <- tab[1,1]
  f22 <- tab[2,2]
  f12 <- tab[1,2]
  f21 <- tab[2,1]
  C1 <- sum(tab[,1])
  C2 <- sum(tab[,2])
  R1 <- sum(tab[1,])
  R2 <- sum(tab[2,])
  n <- sum(R1,R2)
  chis <- (n*(abs(f11*f22-f12*f21)-(n/2))^2)/(C1*C2*R1*R2)
  pvalue <- min(pchisq(chis,1),1-pchisq(chis,1))
  out <- data.frame(chi=round(chis,3),pvalue=round(pvalue,2))
  return(out)
}

chi_square_test(table(ex8_15$number,ex8_15$group))%>%
  kbl(caption = "Result of Chi-square test") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Result of Chi-square test
chi	pvalue
0.473	0.49

빈도표를 생성하여 산출한 통계량은 0.473이고, 자유도가 1인 카이제곱 통계량은 3.841임을 알 수 있다.
통계량이 기각역에 포함되지 않으므로 귀무가설을 기각할 수 없다.
즉, 같은 모집단으로부터 추출된 두 표본의 중위수는 다르다고 할 수 없다.
그러므로 수업 조교에 따른 학생들의 성적 등급의 중위수가 다르다고 할 수 없다.

RVAideMemoire 패키지 내에 있는 mood.medtest() 함수를 사용한 결과를 확인하여 보자.

library(RVAideMemoire)
mood.medtest(ex8_15$data~ex8_15$group,exact=F)

## 
##  Mood's median test
## 
## data:  ex8_15$data by ex8_15$group
## X-squared = 0.47329, df = 1, p-value = 0.4915

gmodels 패키지 내에 있는 CrossTable() 함수를 사용한 결과를 확인하여 보자.

library(gmodels)
CrossTable(ex8_15$number,ex8_15$group, prop.r=F, prop.c=F, prop.t=F, chisq=T,digits=3,prop.chisq=F)

## 
##  
##    Cell Contents
## |-------------------------|
## |                       N |
## |-------------------------|
## 
##  
## Total Observations in Table:  23 
## 
##  
##                  | ex8_15$group 
##    ex8_15$number |  Sample 1 |  Sample 2 | Row Total | 
## -----------------|-----------|-----------|-----------|
##     Above Median |         6 |         6 |        12 | 
## -----------------|-----------|-----------|-----------|
## Not above Median |         3 |         8 |        11 | 
## -----------------|-----------|-----------|-----------|
##     Column Total |         9 |        14 |        23 | 
## -----------------|-----------|-----------|-----------|
## 
##  
## Statistics for All Table Factors
## 
## 
## Pearson's Chi-squared test 
## ------------------------------------------------------------
## Chi^2 =  1.244589     d.f. =  1     p =  0.2645885 
## 
## Pearson's Chi-squared test with Yates' continuity correction 
## ------------------------------------------------------------
## Chi^2 =  0.4732894     d.f. =  1     p =  0.4914778 
## 
## 

EXAMPLE 8.16

Michigan <- c(47,35,7,5,3,2)
Louisiana <- c(48,23,11,13,8,2)
ex8_16 <- data.frame(Michigan,Louisiana)
ex8_16%>%
  kbl(caption = "Dataset",escape=F) %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))

Dataset
Michigan	Louisiana
47	48
35	23
7	11
5	13
3	8
2	2

이 데이터는 미시간 블루제이스의 식단에서 식물성 식품의 빈도와 루이지애나 블루제이스의 식단에서 식물성 식품의 빈도 데이터이다.
독립적인 두개의 표본에 대하여 다양성 지수 차이를 검정하기 위해서는 Shannon index H 를 구하고 허치슨이 제안한 검정통계량을 구하여 검정을 진행하여야 한다.

\[\begin{aligned} H_0 &: H_A = H_2\\ H_A &: H_A \ne H_2 \end{aligned}\]

통계량들을 구하는 공식은 다음과 같다.

\[\begin{aligned} H' &= \frac{n\ \log n\ -\ \sum f_i \log f_i}{n}\\ s_{H'}^2 &=\frac{\sum f_i \log^2 f_i\ -\ (\sum f_i \log^2 f_i)^2/n}{n^2}\\ s_{H_A'-H_2'} &= \sqrt{s_{H_A'}^2+s_{H_2'}^2}\\ t &= \frac{H_A'-H_2'}{s_{H_A'-H_2'}} \sim t(\nu)\\ \nu&=\frac{(s_{H_A'}^2+s_{H_2'}^2)^2}{\frac{(s_{H_A'})^2}{n_1}+\frac{(s_{H_2'})^2}{n_2}} \end{aligned}\]

H_test<- function(x,y){
  n1 <- sum(x)
  filog_1 <- sum(x*log10(x))
  filog2_1 <- sum(x*log10(x)^2)
  h1 <- (n1*log10(n1)-filog_1)/n1
  sh1 <- (filog2_1-(filog_1^2/n1))/n1^2
  n2 <- sum(y)
  filog_2 <- sum(y*log10(y))
  filog2_2 <- sum(y*log10(y)^2)
  h2 <- (n2*log10(n2)-filog_2)/n2
  sh2 <- (filog2_2-(filog_2^2/n2))/n2^2
  s_h1_h2 <- sqrt(sh1+sh2)
  t <- (h1-h2)/s_h1_h2
  v <- (sh1+sh2)^2/( (sh1^2/n1) + (sh2^2/n2) )
  pvalue <- 2*min(pt(t,v),1-pt(t,v))
  if(pvalue < 0.05){
    Reject_H0 <- "yes"
  }else{
    Reject_H0 <- "No"
  }
  out <- data.frame(h1=round(h1,4),h2=round(h2,4),sh1,sh2,s_h1_h2=round(s_h1_h2,4),t=round(t,3),v=round(v),p_value=round(pvalue,3),Reject_H0)
  return(out)
}

H_test(ex8_16$Michigan,ex8_16$Louisiana)%>%
  kbl(caption = "Result of indices of diversity") %>%
  kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive")) 

Result of indices of diversity
h1	h2	sh1	sh2	s_h1_h2	t	v	p_value	Reject_H0
0.5403	0.6328	0.001376	0.0009692	0.0484	-1.909	196	0.058	No

다양성 지수 \(H\) 는 vegan 패키지에 있는 diversity() 함수를 사용해서도 계산이 가능하다.

library(vegan)
h1_1<-diversity(ex8_16$Michigan, index="shannon", base=10)
h2_2<-diversity(ex8_16$Louisiana, index="shannon", base=10)
c(round(h1_1,4),round(h2_2,4))==c(H_test(ex8_16$Michigan,ex8_16$Louisiana)$h1,H_test(ex8_16$Michigan,ex8_16$Louisiana)$h2)

## [1] TRUE TRUE

cat(" diversity() 함수로 구한 다양성 지수 : H1 = ",round(h1_1,4),"  H2 = ",round(h2_2,4),"\n",
    "직접 코딩한 함수로 구한 다양성 지수 : H1 = ",H_test(ex8_16$Michigan,ex8_16$Louisiana)$h1,"  H2 = ",H_test(ex8_16$Michigan,ex8_16$Louisiana)$h2,"\n",
    "두 다양성 지수가 동일한가?  H1 : ",round(h1_1,4)==H_test(ex8_16$Michigan,ex8_16$Louisiana)$h1,"   H2 : ",round(h2_2,4)==H_test(ex8_16$Michigan,ex8_16$Louisiana)$h2)

##  diversity() 함수로 구한 다양성 지수 : H1 =  0.5403   H2 =  0.6328 
##  직접 코딩한 함수로 구한 다양성 지수 : H1 =  0.5403   H2 =  0.6328 
##  두 다양성 지수가 동일한가?  H1 :  TRUE    H2 :  TRUE

다양성 지수 검정 결과 검정통계량 \(t=-1.909\) 이고 \(p-value=0.058\)로 유의수준 0.05보다 크므로 귀무가설 \(H_0\) 를 기각할 충분한 근거를 가지고 있지 않다.
두 Shannon index를 비교해도 미시간 주는 0.5403, 루이지애나는 0.6328로 루이지애나의 식물성 식품에 대한 종 부유도와 종 균등도가 크다고 할수 있겠지만 다양성 지수 검정 결과 미시간 주와 루이지애나 주의 다양성 지수가 같지 않다는 귀무가설을 기각할 충분한 근거가 없다.
그러므로 미시간주와 루이지애나 주의 다양성 지수는 같지 않다는 충분한 근거가 없다.

SAS 프로그램 결과

SAS 접기/펼치기 버튼

8장

LIBNAME ex 'C:\Biostat';
RUN;

/*8장 연습문제 불러오기*/
%MACRO chap08(name=,no=);
%do i=1 %to &no.;
	PROC IMPORT DBMS=excel
		DATAFILE="C:\Biostat\data_chap08"
		OUT=ex.&name.&i. REPLACE;
		RANGE="exam8_&i.$";
	RUN;
%end;
%MEND;

%MACRO chap08_2(name=,no=);
	PROC IMPORT DBMS=excel
		DATAFILE="C:\Biostat\data_chap08"
		OUT=ex.&name.&no. REPLACE;
		RANGE="exam8_&no.$";
	RUN;
%MEND;

%chap08(name=ex8_,no=16);
%chap08_2(name=ex8_,no=2a);

EXAMPLE 8.1

PROC TTEST DATA=ex.ex8_1;
	CLASS drug;
	VAR time;
RUN;

SAS 출력

SAS 시스템

The TTEST Procedure

Variable: time (time)


drug	Method	N	Mean	Std Dev	Std Err	Minimum	Maximum
B		6	8.7500	0.5822	0.2377	7.9000	9.6000
C		7	9.7429	0.8182	0.3093	8.7000	11.1000
Diff (1-2)	Pooled		-0.9929	0.7206	0.4009
Diff (1-2)	Satterthwaite		-0.9929		0.3901


drug	Method	Mean	95% CL Mean		Std Dev	95% CL Std Dev
B		8.7500	8.1390	9.3610	0.5822	0.3634	1.4280
C		9.7429	8.9861	10.4996	0.8182	0.5273	1.8018
Diff (1-2)	Pooled	-0.9929	-1.8753	-0.1105	0.7206	0.5105	1.2235
Diff (1-2)	Satterthwaite	-0.9929	-1.8543	-0.1314


Method	Variances	DF	t Value	Pr > \|t\|
Pooled	Equal	11	-2.48	0.0308
Satterthwaite	Unequal	10.701	-2.55	0.0277


Equality of Variances
Method	Num DF	Den DF	F Value	Pr > F
Folded F	6	5	1.97	0.4722

EXAMPLE 8.2

DATA data; 
SET ex.ex8_2;
RUN;

PROC TTEST order=data sides=L;
	CLASS fertilizer;
	VAR height;
RUN;

SAS 출력

SAS 시스템

The TTEST Procedure

Variable: height (height)


fertilizer	Method	N	Mean	Std Dev	Std Err	Minimum	Maximum
present		10	51.9100	3.3703	1.0658	47.8000	58.3000
newer		8	56.5500	3.1442	1.1116	52.3000	61.3000
Diff (1-2)	Pooled		-4.6400	3.2733	1.5526
Diff (1-2)	Satterthwaite		-4.6400		1.5400


fertilizer	Method	Mean	95% CL Mean		Std Dev	95% CL Std Dev
present		51.9100	49.4990	54.3210	3.3703	2.3182	6.1528
newer		56.5500	53.9214	59.1786	3.1442	2.0788	6.3992
Diff (1-2)	Pooled	-4.6400	-Infty	-1.9293	3.2733	2.4378	4.9817
Diff (1-2)	Satterthwaite	-4.6400	-Infty	-1.9467


Method	Variances	DF	t Value	Pr < t
Pooled	Equal	16	-2.99	0.0043
Satterthwaite	Unequal	15.559	-3.01	0.0042


Equality of Variances
Method	Num DF	Den DF	F Value	Pr > F
Folded F	9	7	1.15	0.8744

EXAMPLE 8.2a

PROC TTEST DATA=ex.ex8_2a;
	CLASS temp;
	VAR days;
RUN;

SAS 출력

SAS 시스템

The TTEST Procedure

Variable: days (days)


temp	Method	N	Mean	Std Dev	Std Err	Minimum	Maximum
10		8	46.0000	9.3503	3.3058	32.0000	59.0000
30		7	37.4286	3.1015	1.1722	32.0000	41.0000
Diff (1-2)	Pooled		8.5714	7.1775	3.7147
Diff (1-2)	Satterthwaite		8.5714		3.5075


temp	Method	Mean	95% CL Mean		Std Dev	95% CL Std Dev
10		46.0000	38.1829	53.8171	9.3503	6.1822	19.0305
30		37.4286	34.5602	40.2969	3.1015	1.9986	6.8296
Diff (1-2)	Pooled	8.5714	0.5463	16.5966	7.1775	5.2034	11.5633
Diff (1-2)	Satterthwaite	8.5714	0.5965	16.5464


Method	Variances	DF	t Value	Pr > \|t\|
Pooled	Equal	13	2.31	0.0381
Satterthwaite	Unequal	8.7104	2.44	0.0380


Equality of Variances
Method	Num DF	Den DF	F Value	Pr > F
Folded F	7	6	9.09	0.0156

EXAMPLE 8.3

DATA exam8_1;
SET ex.ex8_1;
RUN;

PROC IML;
	use exam8_1; read all; close exam8_1;
    exam8_1= TableCreateFromDataSet('exam8_1');
%MACRO n(df);
	sp2=0.5193;
	t=-tinv(0.05 / 2, &df);
	d=0.50 **2;
	n=round((2*sp2*((t)*t)) / d, 1);
	print n;
%MEND n;

%n(98);
%n(32);
%n(34);

n=18;
n1=14;

n2=round(n*n1 / (2*n1-n), 1);

PRINT n2;
QUIT;

SAS 출력

SAS 시스템


n
16


n
17


n
17


n2
25

EXAMPLE 8.4

PROC POWER;
	TWOSAMPLEMEANS TEST=diff alpha=0.05 meandiff=0.5 stddev=0.72 power=0.90 
	npergroup=. ; 
RUN;

PROC IML;
    reset nolong;
	n1=45; 
    n2=30;
    n=(n1*n2)/((2*n2)-n1);
    PRINT n; 
RUN;
QUIT;

SAS 출력

SAS 시스템

The POWER Procedure

Two-Sample t Test for Mean Difference


Fixed Scenario Elements
Distribution	Normal
Method	Exact
Alpha	0.05
Mean Difference	0.5
Standard Deviation	0.72
Nominal Power	0.9
Number of Sides	2
Null Difference	0


Computed N per Group
Actual Power	N per Group
0.903	45

SAS 시스템


n
90

EXAMPLE 8.5

PROC POWER;
	TWOSAMPLEMEANS TEST=diff alpha=0.05 power=0.9 npergroup=20
	stddev=0.7206 meandiff= . ; 
RUN;

SAS 출력

SAS 시스템

The POWER Procedure

Two-Sample t Test for Mean Difference


Fixed Scenario Elements
Distribution	Normal
Method	Exact
Alpha	0.05
Standard Deviation	0.7206
Sample Size per Group	20
Power	0.9
Number of Sides	2
Null Difference	0


Computed Mean Diff
Mean Diff
0.758

EXAMPLE 8.6

PROC POWER;
	TWOSAMPLEMEANS TEST=diff alpha=0.05 power=. npergroup=15
	stddev=0.7206 meandiff=1.0 ; 
RUN;

SAS 출력

SAS 시스템

The POWER Procedure

Two-Sample t Test for Mean Difference


Fixed Scenario Elements
Distribution	Normal
Method	Exact
Alpha	0.05
Mean Difference	1
Standard Deviation	0.7206
Sample Size per Group	15
Number of Sides	2
Null Difference	0


Computed Power
Power
0.956

EXAMPLE 8.7

PROC TTEST DATA=ex.ex8_7;
	CLASS trap;
	VAR number;
RUN;

/*공통분산 구하기*/
DATA trap1; 
SET ex.ex8_7; 
WHERE trap=1;
trap1=1*number;
RUN;

DATA trap2; 
SET ex.ex8_7; 
WHERE trap=2;
trap2=1*number;
RUN;

DATA ex8_7f;
SET trap1 trap2;
RUN;

PROC IML;
	use ex8_7f ; read all;
	v1=var(trap1)*10;
	v2=var(trap2)*9;
	sp=(v1+v2)/(10+9);
PRINT sp;
RUN;
QUIT;

SAS 출력

SAS 시스템

The TTEST Procedure

Variable: number (number)


trap	Method	N	Mean	Std Dev	Std Err	Minimum	Maximum
1		11	36.4545	4.6768	1.4101	30.0000	46.0000
2		10	57.7000	3.5917	1.1358	52.0000	64.0000
Diff (1-2)	Pooled		-21.2455	4.1979	1.8342
Diff (1-2)	Satterthwaite		-21.2455		1.8106


trap	Method	Mean	95% CL Mean		Std Dev	95% CL Std Dev
1		36.4545	33.3126	39.5965	4.6768	3.2678	8.2075
2		57.7000	55.1307	60.2693	3.5917	2.4705	6.5570
Diff (1-2)	Pooled	-21.2455	-25.0845	-17.4064	4.1979	3.1925	6.1314
Diff (1-2)	Satterthwaite	-21.2455	-25.0418	-17.4491


Method	Variances	DF	t Value	Pr > \|t\|
Pooled	Equal	19	-11.58	<.0001
Satterthwaite	Unequal	18.522	-11.73	<.0001


Equality of Variances
Method	Num DF	Den DF	F Value	Pr > F
Folded F	10	9	1.70	0.4401

SAS 시스템


sp
17.622488

EXAMPLE 8.8

PROC TTEST DATA=ex.ex8_8;
	CLASS site;
	VAR time;
RUN;

/*정규성 검정*/
PROC UNIVARIATE DATA=ex.ex8_8 normal;
	CLASS site;
	VAR time;
RUN;

SAS 출력

SAS 시스템

The TTEST Procedure

Variable: time (time)


site	Method	N	Mean	Std Dev	Std Err	Minimum	Maximum
1		7	75.4143	3.8852	1.4685	69.3000	81.0000
2		9	78.3778	9.3607	3.1202	64.6000	93.9000
Diff (1-2)	Pooled		-2.9635	7.5192	3.7893
Diff (1-2)	Satterthwaite		-2.9635		3.4485


site	Method	Mean	95% CL Mean		Std Dev	95% CL Std Dev
1		75.4143	71.8211	79.0075	3.8852	2.5036	8.5555
2		78.3778	71.1825	85.5730	9.3607	6.3227	17.9329
Diff (1-2)	Pooled	-2.9635	-11.0908	5.1638	7.5192	5.5050	11.8586
Diff (1-2)	Satterthwaite	-2.9635	-10.5368	4.6098


Method	Variances	DF	t Value	Pr > \|t\|
Pooled	Equal	14	-0.78	0.4472
Satterthwaite	Unequal	11.204	-0.86	0.4082


Equality of Variances
Method	Num DF	Den DF	F Value	Pr > F
Folded F	8	6	5.80	0.0459

SAS 시스템

UNIVARIATE 프로시저

변수: time (time)

site = 1


적률
N	7	가중합	7
평균	75.4142857	관측값 합	527.9
표준 편차	3.88519779	분산	15.0947619
왜도	-0.1927366	첨도	-0.1099754
제곱합	39901.77	수정 제곱합	90.5685714
변동계수	5.15180613	평균의 표준 오차	1.46846674


기본 통계 측도
위치측도		변이측도
평균	75.41429	표준 편차	3.88520
중위수	75.50000	분산	15.09476
최빈값	.	범위	11.70000
		사분위수 범위	6.40000


위치모수 검정: Mu0=0
검정	통계량		p 값
스튜던트의 t	t	51.3558	Pr > \|t\|	<.0001
부호	M	3.5	Pr >= \|M\|	0.0156
부호 순위	S	14	Pr >= \|S\|	0.0156


정규성 검정
검정	통계량		p 값
Shapiro-Wilk	W	0.990114	Pr < W	0.9934
Kolmogorov-Smirnov	D	0.141352	Pr > D	>0.1500
Cramer-von Mises	W-Sq	0.019144	Pr > W-Sq	>0.2500
Anderson-Darling	A-Sq	0.134195	Pr > A-Sq	>0.2500


분위수(정의 5)
레벨	분위수
100% 최댓값	81.0
99%	81.0
95%	81.0
90%	81.0
75% Q3	78.7
50% 중위수	75.5
25% Q1	72.3
10%	69.3
5%	69.3
1%	69.3
0% 최솟값	69.3


극 관측값
최소		최대
값	관측값	값	관측값
69.3	1	74.7	4
72.3	5	75.5	2
74.7	4	76.4	7
75.5	2	78.7	6
76.4	7	81.0	3

SAS 시스템

UNIVARIATE 프로시저

변수: time (time)

site = 2


적률
N	9	가중합	9
평균	78.3777778	관측값 합	705.4
표준 편차	9.3606594	분산	87.6219444
왜도	0.27087297	첨도	-0.6762365
제곱합	55988.66	수정 제곱합	700.975556
변동계수	11.9430018	평균의 표준 오차	3.1202198


기본 통계 측도
위치측도		변이측도
평균	78.37778	표준 편차	9.36066
중위수	76.00000	분산	87.62194
최빈값	.	범위	29.30000
		사분위수 범위	11.40000


위치모수 검정: Mu0=0
검정	통계량		p 값
스튜던트의 t	t	25.11931	Pr > \|t\|	<.0001
부호	M	4.5	Pr >= \|M\|	0.0039
부호 순위	S	22.5	Pr >= \|S\|	0.0039


정규성 검정
검정	통계량		p 값
Shapiro-Wilk	W	0.978589	Pr < W	0.9566
Kolmogorov-Smirnov	D	0.155815	Pr > D	>0.1500
Cramer-von Mises	W-Sq	0.025996	Pr > W-Sq	>0.2500
Anderson-Darling	A-Sq	0.159011	Pr > A-Sq	>0.2500


분위수(정의 5)
레벨	분위수
100% 최댓값	93.9
99%	93.9
95%	93.9
90%	93.9
75% Q3	84.8
50% 중위수	76.0
25% Q1	73.4
10%	64.6
5%	64.6
1%	64.6
0% 최솟값	64.6


극 관측값
최소		최대
값	관측값	값	관측값
64.6	9	76.0	12
69.5	8	81.2	14
73.4	15	84.8	11
74.0	10	88.0	16
76.0	12	93.9	13

EXAMPLE 8.9

**필요값 계산**;
PROC IML;
	type1={41,35,33,36,40,46,31,37,34,30,38};
	type2={52,57,62,55,64,57,56,55,60,59};
	n1=nrow(type1);
	n2=nrow(type2);
	v1=n1-1;
	v2=n2-1;
	sum1=sum(type1);
	sum2=sum(type2);
	xbar1=round(sum1 / n1, 0.01);
	xbar2=sum2 / n2;

	xprime1=repeat(0,1,n1);
		do i=1 to n1 by 1;
		xprime1[i]=abs(type1[i]-xbar1);
		end;
	xprime2=repeat(0,1,n2);
		do i=1 to n2 by 1;
		xprime2[i]=abs(type2[i]-xbar2);
		end;
	s_xprime1=sum(xprime1);
	s_xprime2=sum(xprime2);
	xprim1=round(s_xprime1 / n1, 0.01);
	xprim2=s_xprime2 / n2;
    SS_1 = 77.25;
	SS_2 = 35.44;

	sp_prime=round((SS_1+SS_2) / (v1+v2), 0.01);
	s_differ=round(sqrt(sp_prime/n1 + sp_prime/n2), 0.01);
	t_prime=round((xprim1-xprim2) / s_differ, 0.01);
	t_19=round(-tinv(0.05 / 2, 19), 0.001);
	PRINT sp_prime s_differ t_prime t_19;
QUIT;

ods graphics off;ods exclude all;ods noresults;
PROC GLM DATA=ex.ex8_7;
	CLASS trap;
	MODEL number=trap;
	MEANS trap / hovtest=levene(type=abs);
	ods output HOVFTest=HOVFTest;
RUN;
QUIT;
ods graphics on;ods exclude none;ods results;

PROC PRINT DATA=HOVFTest;
RUN;

SAS 출력

SAS 시스템

sp_prime	s_differ	t_prime	t_19
5.93	1.06	0.71	2.093

SAS 시스템


OBS	Effect	Dependent	Method	Source	DF	SS	MS	FValue	ProbF
1	trap	number	LV	trap	1	2.9212	2.9212	0.49	0.4913
2	trap	number	LV	Error	19	112.7	5.9293	_	_

EXAMPLE 8.10

**필요값 계산**;
**(a)**;
PROC IML;
	weight={72.5,71.7,60.8,63.2,71.4,73.1,77.9,75.7,72.0,69.0};
	height={183.0,172.3,180.1,190.2,191.4,169.6,166.4,177.6,184.7,187.5,179.8};
	n1=nrow(weight); n2=nrow(height);
	v1=n1-1; v2=n2-1;
	sum1=sum(weight); sum2=sum(height);
	xbar1=sum1 / n1; xbar2=sum2 / n2;
	sum_squares1=sum(t(weight) * weight);
	sum_squares2=sum(t(height) * height);
    SS_1 = round(sum_squares1 - sum1**2 /n1, 0.0001);
	SS_2 = round(sum_squares2 - sum2**2 /n2, 0.0001);
	s2_1= round(SS_1 / (n1-1),0.0001);
	s2_2 = round(SS_2 / (n2-1),0.0001);
	s1=round(sqrt(s2_1), 0.01);
	s2=round(sqrt(s2_2), 0.01);
	cv1=round(s1 / xbar1, 0.0001);
	cv2=round(s2 / xbar2, 0.0001);

	logx=repeat(0,n1,1);
		DO i=1 TO n1 BY 1;
		logx[i]=round(log10(weight[i]), 0.00001);
		END;
	logy=repeat(0,n2,1);
		DO i=1 TO n2 BY 1;
		logy[i]=round(log10(height[i]), 0.00001);
		END;

	suml1=sum(logx); suml2=sum(logy);
	sum_squaresl1=sum(t(logx) * logx);
	sum_squaresl2=sum(t(logy) * logy);
    SS_logx = round(sum_squaresl1 - suml1**2 /n1, 0.000000001);
	SS_logy = round(sum_squaresl2 - suml2**2 /n2, 0.000000001);
	s_logx=round(var(logx), 0.0000001);
	s_logy=round(var(logy), 0.0000001);
	F=round(s_logx / s_logy, 0.01);
	F_2=round(quantile("F", 1-(0.05 / 2), 9,10), 0.01);
    
    
**(b)**;
	Vp=round((v1*cv1 + v2*cv2) / (v1+v2), 0.0001);
	Vp2= round(Vp**2,0.00001);
	Z=round((cv1-cv2)/sqrt(((Vp2 / v1)+(Vp2 / v2))*(0.5+Vp2)),0.01);
	Z_2=round(abs(quantile("Normal", 0.05 / 2)), 0.01);
	PRINT cv1 cv2 F F_2 Vp Vp2 Z Z_2;
QUIT;

**ttest**;
DATA weight;
SET ex.ex8_10;
IF weight =. THEN DELETE;
weight_or_height = weight;
group=1;
KEEP group weight_or_height;
RUN;

DATA height;
SET ex.ex8_10;
IF height =. THEN DELETE;
weight_or_height = height;
group=2;
KEEP group weight_or_height;
RUN;

DATA exam8_10_ttest;
SET weight height;
RUN;

ods graphics off;ods exclude all;ods noresults;
PROC TTEST DATA=exam8_10_ttest dist=lognormal;
CLASS group;
VAR weight_or_height;
ODS OUTPUT Equality = CV_test;
RUN;
ods graphics on;ods exclude none;ods results;
PROC PRINT DATA=CV_test LABEL;
RUN;

SAS 출력

SAS 시스템

cv1	cv2	F	F_2	Vp	Vp2	Z	Z_2
0.0739	0.0457	2.74	3.78	0.0591	0.00349	1.46	1.96

SAS 시스템


OBS	Variable	Method	Numerator Degrees Freedom	Denominator Degrees Freedom	F Value	Pr > \|F\|
1	weight_or_height	Folded F	9	10	2.74	0.1322

EXAMPLE 8.11

TITLE 'Example 8.11: 방법1 Wilcoxon Two-Sample Test';
%MACRO wilcoxon(data, class, var);
ods graphics off;
ods exclude all;
ods noresults;
PROC NPAR1WAY DATA=&data wilcoxon;
	EXACT wilcoxon;
	CLASS &class;
	VAR &var;
	ods output WilcoxonTest = wilcoxon_test;
RUN;
ods graphics on;
ods exclude none;
ods results;
PROC PRINT DATA=wilcoxon_test label;
RUN;
%MEND;
%wilcoxon(ex.ex8_11, sex, height);

PROC RANK DATA=ex.ex8_11 out=ex8_11_rank descending;
VAR height;
RANKS rank;
RUN;

TITLE 'Rank of male heights';
PROC PRINT DATA=ex8_11_rank;
WHERE sex=1;
RUN;

TITLE 'Rank of female heights';
PROC PRINT DATA=ex8_11_rank;
WHERE sex=2;
RUN;

TITLE 'Example 8.11: 방법2';
PROC IML;
USE ex8_11_rank;
READ all;
CLOSE ex8_11_rank;

male = loc(sex=1);
female = loc(sex=2);

n1= nrow( sex[male]);
n2= nrow( sex[female]);
R1 = sum(rank[male]);
R2 = sum(rank[female]);

U = n1*n2 + n1*(n1+1)/2 - R1;
U_prime = n1*n2 - U;

*print n1 n2 R1 R2 U U_prime;
PRINT U U_prime;
RUN;
QUIT;

SAS 출력

Example 8.11: 방법1 Wilcoxon Two-Sample Test


OBS	Variable	Statistic (S)	Z	Pr < Z	Pr > \|Z\|	t Approximation Pr < Z	t Approximation Pr > \|Z\|	Exact Pr <= S	Exact Pr >= \|S - Mean\|
1	height	18.0000	-2.2736	0.0115	0.0230	0.0220	0.0440	0.0088	0.0177

Rank of male heights


OBS	sex	height	rank
1	1	193	1
2	1	188	2
3	1	185	3
4	1	183	4
5	1	180	5
6	1	175	7
7	1	170	9

Rank of female heights


OBS	sex	height	rank
8	2	178	6
9	2	173	8
10	2	168	10
11	2	165	11
12	2	163	12

Example 8.11: 방법2

U	U_prime
32	3

EXAMPLE 8.12

title 'Example 8.12 : 방법1';
DATA ex8_12;
INPUT training speed @@;
CARDS;
1 44 1 48 1 36 1 32  1 51 1 45 1 54 1 56 
2 32 2 40 2 44 2 44 2 34 2 30 2 26
;
RUN;
%wilcoxon(ex8_12, training, speed);

PROC RANK DATA=ex8_12 out=ex8_12_rank;
	VAR speed;
	RANKS rank;
RUN;

TITLE 'With training (rank in parentheses)';
PROC PRINT DATA=ex8_12_rank;
	WHERE training = 1;
RUN;

TITLE 'Without training (rank in parentheses)';
PROC PRINT DATA=ex8_12_rank;
	WHERE training = 2;
RUN;

PROC IML;
USE ex8_12_rank;
READ all;
CLOSE ex8_12_rank;
group1 = loc(training=1);
group2 = loc(training=2);

n1 = nrow(training[group1]);
n2 = nrow(training[group2]);
R1 = sum(rank[group1]);
R2 = sum(rank[group2]);

U_prime = n1*n2 + n2*(n2+1)/2 - R2;

TITLE 'Example 8.12 : 방법2';
PRINT R1 R2 U_prime ;
RUN;
QUIT;

SAS 출력

Example 8.12 : 방법1


OBS	Variable	Statistic (S)	Z	Pr < Z	Pr > \|Z\|	t Approximation Pr < Z	t Approximation Pr > \|Z\|	Exact Pr <= S	Exact Pr >= \|S - Mean\|
1	speed	36.5000	-2.2087	0.0136	0.0272	0.0222	0.0444	0.0106	0.0211

With training (rank in parentheses)


OBS	training	speed	rank
1	1	44	9.0
2	1	48	12.0
3	1	36	6.0
4	1	32	3.5
5	1	51	13.0
6	1	45	11.0
7	1	54	14.0
8	1	56	15.0

Without training (rank in parentheses)


OBS	training	speed	rank
9	2	32	3.5
10	2	40	7.0
11	2	44	9.0
12	2	44	9.0
13	2	34	5.0
14	2	30	2.0
15	2	26	1.0

Example 8.12 : 방법2

R1	R2	U_prime
83.5	36.5	47.5

EXAMPLE 8.13

title 'Example 8.13';
PROC IML;
n1=22;
n2=46;
N = n1+n2;
U=282;

U_prime = n1*n2 - U;
mu_U = (n1*n2)/2;
sigma_U = round(sqrt((n1*n2*(N+1))/12), 0.01);
Z = round((U_prime-mu_U)/sigma_U, 0.01);
Z_criticalvalue=round(quantile('NORMAL', 1-0.05), 0.0001);
Z_pvalue = round(1-cdf('NORMAL', Z), 0.0001);

*print U U_prime mu_U sigma_U ; 
PRINT Z Z_criticalvalue Z_pvalue;
RUN;
QUIT;

SAS 출력

Example 8.13

Z	Z_criticalvalue	Z_pvalue
2.94	1.6449	0.0016

EXAMPLE 8.14

title 'Example 8.14 : 방법1';
DATA exam8_14;
INPUT assistant rank @@;
CARDS;
1 3 1 3 1 3 1 6 1 10 1 10 1 13.5 1 13.5 1 16.5 1 16.5 1 19.5
2 3 2 3 2 7.5 2 7.5 2 10 2 12 2 16.5 2 16.5 2 19.5 2 22.5 2 22.5 2 22.5 2 22.5 2 25
;
RUN;
%wilcoxon(exam8_14, assistant, rank);

SAS 출력

Example 8.14 : 방법1


OBS	Variable	Statistic (S)	Z	Pr < Z	Pr > \|Z\|	t Approximation Pr < Z	t Approximation Pr > \|Z\|	Exact Pr <= S	Exact Pr >= \|S - Mean\|
1	rank	114.5000	-1.5469	0.0609	0.1219	0.0675	0.1350	0.0604	0.1213

EXAMPLE 8.15

DATA ex8_15;
INPUT group $ sample x @@;
CARDS;
a 1 6 a 2 6 n 1 3 n 2 8
;
RUN;

DATA  data; 
SET  ex8_15;
RUN;

PROC FREQ order=data;
	WEIGHT x;
	TABLE group*sample/expected chisq;
RUN;

SAS 출력

Example 8.14 : 방법1

FREQ 프로시저

빈도 기대값 백분율 행 백분율 칼럼 백분율


테이블 group * sample
group	sample
group	1	2	합계
a	6 4.6957 26.09 50.00 66.67	6 7.3043 26.09 50.00 42.86	12 52.17
n	3 4.3043 13.04 27.27 33.33	8 6.6957 34.78 72.73 57.14	11 47.83
합계	9 39.13	14 60.87	23 100.00

group * sample 테이블에 대한 통계량


통계량	자유도	값	Prob
WARNING: 50%개의 셀이 5보다 적은 기대빈도를 가지고 있습니다. 카이제곱 검정은 올바르지 않을 수 있습니다.
카이제곱	1	1.2446	0.2646
우도비 카이제곱	1	1.2626	0.2612
연속성 수정 카이제곱	1	0.4733	0.4915
Mantel-Haenszel 카이제곱	1	1.1905	0.2752
파이 계수		0.2326
우발성 계수		0.2266
크래머의 V		0.2326


Fisher의 정확 검정
(1,1) 셀 빈도(F)	6
하단측 p값 Pr <= F	0.9398
상단측 p값 Pr >= F	0.2468

테이블 확률 (P)	0.1866
양측 p값 Pr <= P	0.4003

표본 크기 = 23

EXAMPLE 8.16

PROC IML;
	RESET nolog;
	michigan={47, 35, 7,5,3,2};
	m_log=michigan#(log10(michigan));
	m_log2=michigan#(log10(michigan)) # (log10(michigan));

	louisiana={48,23,11,13,8,2};
	lou_log=louisiana#(log10(louisiana));
	lou_log2=louisiana#(log10(louisiana)) # (log10(louisiana));

	sh1=((sum(m_log2))-((sum(m_log))**2)/sum(michigan))/sum(michigan)**2;
	sh2=((sum(lou_log2))-((sum(lou_log))**2)/sum(louisiana))/sum(louisiana)**2;

	sh_f=sh1+sh2;
	sh_ff=sqrt(sh1+sh2);

	t=(0.5403-0.6328)/sh_ff;

	v=((sh_f)**2)/((((sh1)**2)/99)+(((sh2)**2)/105));

	p=probt(-1.911, v)*2;

	PRINT sh_ff  v p;

RUN;
QUIT;

SAS 출력

Example 8.14 : 방법1

sh_ff	v	p
0.0484277	195.92776	0.0574643

교재: Biostatistical Analysis (5th Edition) by Jerrold H. Zar

**이 글은 22학년도 1학기 의학통계방법론 과제 자료들을 정리한 글 입니다.**

exam8_2a.temp	exam8_2a.days
30	40
30	38
30	32
30	37
30	39
30	41
30	35
10	36
10	45
10	32
10	52
10	59
10	41
10	48
10	55

exam8_2a.temp	exam8_2a.days
30	40
30	38
30	32
30	37
30	39
30	41
30	35
10	36
10	45
10	32
10	52
10	59
10	41
10	48
10	55

Two-Sample Hypotheses

R 프로그램 결과

8장

EXAMPLE 8.1

EXAMPLE 8.2

EXAMPLE 8.2a

EXAMPLE 8.3

EXAMPLE 8.4

EXAMPLE 8.5

EXAMPLE 8.6

EXAMPLE 8.7

EXAMPLE 8.8

EXAMPLE 8.9

EXAMPLE 8.10

EXAMPLE 8.11

EXAMPLE 8.12

EXAMPLE 8.13

EXAMPLE 8.14

EXAMPLE 8.15

EXAMPLE 8.16

SAS 프로그램 결과

8장

EXAMPLE 8.1

EXAMPLE 8.2

EXAMPLE 8.2a

EXAMPLE 8.3

EXAMPLE 8.4

EXAMPLE 8.5

EXAMPLE 8.6

EXAMPLE 8.7

EXAMPLE 8.8

EXAMPLE 8.9

EXAMPLE 8.10

EXAMPLE 8.11

EXAMPLE 8.12

EXAMPLE 8.13

EXAMPLE 8.14

EXAMPLE 8.15

EXAMPLE 8.16

Templates (for web app):

Error

exam8_2a.temp	exam8_2a.days
30	40
30	38
30	32
30	37
30	39
30	41
30	35
10	36
10	45
10	32
10	52
10	59
10	41
10	48
10	55