[의학통계방법론] Ch4. Measures of Variability and Dispersion
Measures of Variability and Dispersion
R 프로그램 결과
R 접기/펼치기 버튼
패키지 설치된 패키지 접기/펼치기 버튼
getwd()
## [1] "C:/Biostat"
library("Hmisc")
library("readxl")
library("ggplot2")
library("vegan")
library("dplyr")
엑셀파일불러오기
#모든 시트를 하나의 리스트로 불러오는 함수
read_excel_allsheets <- function(file, tibble = FALSE) {
sheets <- readxl::excel_sheets(file)
x <- lapply(sheets, function(X) readxl::read_excel(file, sheet = X))
if(!tibble) x <- lapply(x, as.data.frame)
names(x) <- sheets
x
}
4장
4장 연습문제 불러오기
#data_chap04에 연습문제 4장 모든 문제 저장
data_chap04 <- read_excel_allsheets("data_chap04.xls")
#연습문제 각각 데이터 생성
for (x in 1:length(data_chap04)){
assign(paste0('ex4_',1:length(data_chap04))[x],data_chap04[x])
}
#연습문제 데이터 형식을 리스트에서 데이터프레임으로 변환
for (x in 1:length(data_chap04)){
assign(paste0('ex4_',1:length(data_chap04))[x],data.frame(data_chap04[x]))
}
EXAMPLE 4.1

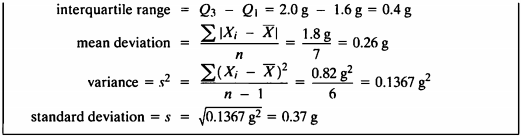
#데이터셋
ex4_1
## exam4_1.X1 exam4_1.X2
## 1 1.2 1.2
## 2 1.4 1.6
## 3 1.6 1.7
## 4 1.8 1.8
## 5 2.0 1.9
## 6 2.2 2.0
## 7 2.4 2.4
library(tibble)
sample1 <- ex4_1$exam4_1.X1 ; sample2 <- ex4_1$exam4_1.X2
f4_1 <- function(x) {
x <- na.omit(x)
n <- length(x) #빈도
range <- max(x) - min(x) #범위
mean <- mean(x) #평균
iqr <- IQR(x, type=1) #IQR
mdev <- round(sum(abs(x-mean(x)))/length(x),2) #평균편차
var <- round(var(x), 4) #분산
sd <- round(sd(x), 2) #표준편차
sos <- sum((x-mean(x))^2) #Sum of Squares
out <- data.frame(n=n, Mean=mean, Range=range, IQR=iqr, Mean_deviance=mdev, Variance=var, Standard_deviantion=sd, Sum_of_Squares = sos)
return(out)
}
s1 <- f4_1(sample1) ; s2 <- f4_1(sample2)
nn <- tibble(data=c("Sample1","Sample2"))
s3 <- rbind(s1,s2) ; s4 <- data.frame(nn,s3)
s4
## data n Mean Range IQR Mean_deviance Variance Standard_deviantion
## 1 Sample1 7 1.8 1.2 0.8 0.34 0.1867 0.43
## 2 Sample2 7 1.8 1.2 0.4 0.26 0.1367 0.37
## Sum_of_Squares
## 1 1.12
## 2 0.82
| \(Sample \space 1\) | \(Sample \space 2\) | |
|---|---|---|
| Sample Size | 7g | 7g |
| Mean | 1.8g | 1.8g |
| Range | 1.2g | 1.2g |
| Interquartile Range | 0.8g | 0.4g |
| Mean Deviation | 0.34g | 0.26g |
| Variance | 0.1867g2 | 0.1367g2 |
| Standard Deviation | 0.43g | 0.37g |
| Sum of Squares | 1.12g2 | 0.82g2 |
범위는 가장 높은 측정값과 가장 낮은 측정값을 제외한 어떤 측정값도 고려하지 않는다는 점에서 비교적 조잡한 분산 측정값이다.
또한 표본이 모집단에서 가장 높은 값과 가장 낮은 값을 모두 포함할 가능성은 낮으므로 표본 범위는 일반적으로 모집단 범위를 과소평가(underestimate)한다.
따라서 표본 범위는 편향되고 비효율적인 추정치이다.
그럼에도 불구하고 일부에서는 표본 범위를 모집단 범위의 추정치(비록 좋지 않다.)로 제시하는 것이 유용한 것으로 간주하기도 한다.
예를 들어, 분류학자들(taxonomists)은 종종 모집단에서 가장 높은 값과 가장 낮은 값의 추정치를 갖는 것에 관심이 있다.
그러나 보고 데이터에 범위가 지정될 때마다 다른 분산 측정값들도 함께 보고하는 것이 좋다.
(범위는 순서형, 구간 및 비율 척도 데이터에 적용할 수 있다.)
EXAMPLE 4.2

#데이터셋
ex4_2
## exam4_2.X1 exam4_2.X2
## 1 1.2 1.2
## 2 1.4 1.6
## 3 1.6 1.7
## 4 1.8 1.8
## 5 2.0 1.9
## 6 2.2 2.0
## 7 2.4 2.4
sample1 <- ex4_2$exam4_2.X1 ; sample2 <- ex4_2$exam4_2.X2
f4_2 <- function(x) {
sumxi <- sum(x)
sumxi2 <- sum(x^2)
n <- length(x)
xbar <- mean(x)
ss <- sum(x^2)-(sum(x)^2/length(x))
s2 <- (sum(x^2)-(sum(x)^2/length(x)))/(length(x)-1)
s <-sqrt((sum(x^2)-(sum(x)^2/length(x)))/(length(x)-1))
v <- (sqrt((sum(x^2)-(sum(x)^2/length(x)))/(length(x)-1)))/(mean(x))
out <- data.frame(Sum_Xi=sumxi,Sum_xi2=round(sumxi2,2),n=n,Mean=xbar,SS=ss,s2=round(s2,4),s=round(s,2),V=round(v,2))
return(out)
}
s1 <- f4_2(sample1)
s2 <- f4_2(sample2)
nn <- tibble(data=c("Sample1","Sample2"))
s3 <- rbind(s1,s2);s4 <- data.frame(nn,s3)
s4
## data Sum_Xi Sum_xi2 n Mean SS s2 s V
## 1 Sample1 12.6 23.8 7 1.8 1.12 0.1867 0.43 0.24
## 2 Sample2 12.6 23.5 7 1.8 0.82 0.1367 0.37 0.21
| \(Sample \space 1\) | \(Sample \space 2\) | |
|---|---|---|
| ∑Xi | 12.6g | 12.6g |
| ∑Xi2 | 23.8g | 23.5g |
| \(Sample\space size\) | 7g | 7g |
| \(\overline X\) | 1.8g | 1.8g |
| SS | 1.12g2 | 1.12g2 |
| s2 | 0.1867g2 | 0.1367g2 |
| s | 0.43g | 0.37g |
| \(Coefficient \space of \space Variance\) | 24% | 21% |
마지막에 변동계수를 보면 Sample1은 24%이고 Sample2는 21%이다.
이는 sample1의 변동이 sample2보다 크다는 것을 의미하며
변동계수는 산포의 정규화된 측도라 하며 평균에 대한 표준편차의 비로 정의한다.
변동계수를 구하는 식은 다음과 같다.
(이는 데이터의 실제 크기나 측정 단위와는 별개로 상대적인 측정치임을 강조한다.)
변동 계수는 비율 척도 데이터에 대해서만 계산할 수 있다.
(예를 들어 섭씨 또는 화씨 온도 척도에서 측정된 온도 데이터의 변동 계수를 계산하는 것은 유효하지 않다.)
EXAMPLE 4.3


#데이터셋
ex4_3
## exam4_3.Sites exam4_3.Sample1 exam4_3.Sample2 exam4_3.Sample3
## 1 Vines 5 1 2
## 2 Eaves 5 1 2
## 3 Branches 5 1 2
## 4 Cavities 5 17 34
그 중 관련 지수로는 Shannon-Wiener diversity index *H*′ 가 있다.
이론적으로, 최대 가능한 다양성 지수는 카테고리의 개수 *k* 로 구성되며 다음의 식으로 계산된다.
library(vegan)
sam1 <- ex4_3$exam4_3.Sample1 ; sam2 <- ex4_3$exam4_3.Sample2 ; sam3 <- ex4_3$exam4_3.Sample3
f4_3 <- function(x) {
n <- sum(x)
H <- round(diversity(x,base=10),3)
H_max <- round(log10(length(x)),3)
J <- round(H / H_max,2)
out <- data.frame(H=H, H_max = H_max, J=round(J,2))
return(out)
}
h1<-f4_3(sam1) ; h2<-f4_3(sam2) ; h3<-f4_3(sam3)
nn <- tibble(data=c("Sample 1","Sample 2","Sample 3"))
h4 <- rbind(h1,h2,h3);h4 <- data.frame(nn,h4)
h4
## data H H_max J
## 1 Sample 1 0.602 0.602 1.00
## 2 Sample 2 0.255 0.602 0.42
## 3 Sample 3 0.255 0.602 0.42
| \(Sample\ 1\) | \(Sample\ 2\) | \(Sample\ 3\) | |
|---|---|---|---|
| \(Sample\ Size\) | 20 | 20 | 40 |
| \(H'\) | 0.602 | 0.255 | 0.255 |
| \(H'_{max}\) | 0.602 | 0.602 | 0.602 |
| \(J'\) | 1 | 0.42 | 0.42 |
데이터의 카테고리의 개수는 전형적으로 모집단으로부터 과소평가되는데 이는 데이터를 수집하는 경우에 몇몇의 카테고리를 수집하지 않을 수 있기 때문이다.
그러므로 종의 균등성을 나타내는 *J*′ 는 전형적으로 모집단의 종균등성의 과대평가되는 지표라 할 수 있다.
보통 종 부유도와 종 균등도가 클수록 *H*′ 가 증가하고 *J*′ 도 증가하는데
해당 데이터의 결과를 보면 Sample 1 의 *H*′는 0.6021이고 *J*′가 1이다.
나머지 Sample 2와 Sample 3sms 각각 *H*′가 0.255로 *J*′가 0.42로 Sample 1보다 작은것을 볼 수 있다.
*종 균등비율 높을수록, Shannon Index(다양성 지표)와 J’(균등도 지표) 커지는 것을 알 수 있다.*
EXAMPLE 4.4
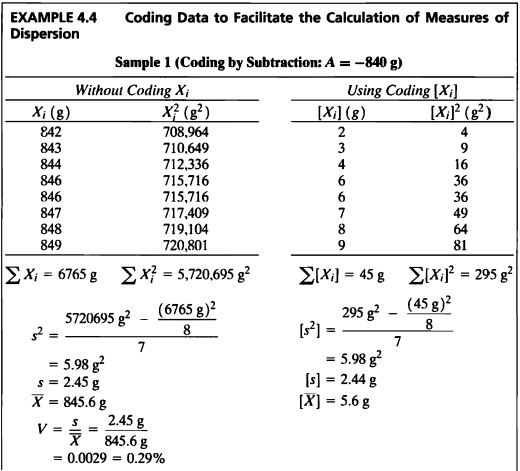
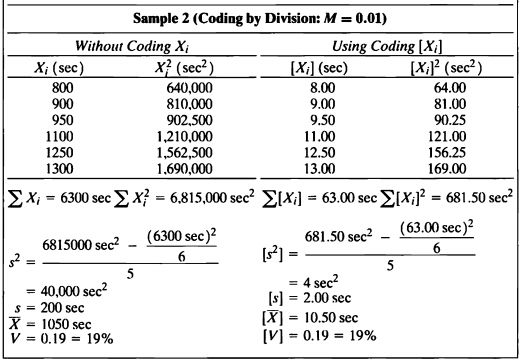
#데이터셋
ex4_4
## exam4_4.X1 exam4_4.code1 exam4_4.X2 exam4_4.code2 exam4_4.X3 exam4_4.code3
## 1 842 2 708964 4 800 8.0
## 2 843 3 710649 9 900 9.0
## 3 844 4 712336 16 950 9.5
## 4 846 6 715716 36 1100 11.0
## 5 846 6 715716 36 1250 12.5
## 6 847 7 717409 49 1300 13.0
## 7 848 8 719104 64 NA NA
## 8 849 9 720801 81 NA NA
## exam4_4.X4 exam4_4.code4
## 1 640000 64.00
## 2 810000 81.00
## 3 902500 90.25
## 4 1210000 121.00
## 5 1562500 156.25
## 6 1690000 169.00
## 7 NA NA
## 8 NA NA
x1<-ex4_4$exam4_4.X1 ; code1 <- ex4_4$exam4_4.code1
x3 <- na.omit(ex4_4$exam4_4.X3) ; code3 <- na.omit(ex4_4$exam4_4.code3)
f4_4 <- function(x) {
n <- length(x)
sumx <- sum(x)
ss <- sum(x^2)
s2 <- round((ss - sumx^2 / n) / (n-1), 2)
s <- round(sqrt(s2), 2)
mean <- round(mean(x),1)
v <- round(s / mean,4)
out <- data.frame(sum = sumx, sum_of_squares = ss, Variance = s2, Standard_deviation=s, Mean=mean, CV=v)
return(out)
}
nn <- tibble(data=c("X 1","Code 1","X 3","Code 3"))
vv <- rbind(f4_4(x1),f4_4(code1),f4_4(x3),f4_4(code3))
vv <- data.frame(nn,vv)
vv
## data sum sum_of_squares Variance Standard_deviation Mean CV
## 1 X 1 6765 5720695.0 5.98 2.45 845.6 0.0029
## 2 Code 1 45 295.0 5.98 2.45 5.6 0.4375
## 3 X 3 6300 6815000.0 40000.00 200.00 1050.0 0.1905
## 4 Code 3 63 681.5 4.00 2.00 10.5 0.1905
| \(Sample\ 1\) | \(Sample\ 2\) | |
|---|---|---|
| Sample Size | 8 g | 6 g |
| Sum of X | 6765 g | 6300 g |
| Sum of X2 | 5720695 g2 | 6815000 g2 |
| s2 | 5.98 g2 | 40000 g2 |
| s | 2.45 g | 200 g |
| Mean | 845.6 g | 1050 g |
| CV | 0.29 % | 19 % |
| —————— | ——– | ——– |
| Sum of coding X | 45 g | 63 g |
| sum of coding X2 | 295 g2 | 681.5 g2 |
| coding s2 | 5.98 g2 | 4 g |
| coding s | 2.45 g | 2 g |
| coding Mean | 5.625 g | 10.5 g |
| coding CV | 44 % | 19 % |
(*A* = − 840) 이는 원래 데이터의 평균에 *A* 만큼 더한 만큼 차이가나 동일하다.
Sample 2에서도 마찬가지로 *M* = 0.01 을 곱한 만큼 차이가나 동일한 것을 볼 수 있다.
차이점은 변동계수에서 난다.
두 데이터 모두 코딩 전 후의 분산 및 표준편차가 동일하지만 Sample 1 을 보면 변동계수의 차이가 나며
Sample 2와 같이 곱셈 및 나눗셈으로 코딩된 경우에는 차이가 나지 않음을 확인할 수 있다.
*상수 A를 더하거나 빼면 분산, 표준편차는 변하지 않지만,*
*상수 M을 곱하면 분산, 표준편차가 변하는 것을 알 수 있다.*
SAS 프로그램 결과
SAS 접기/펼치기 버튼
4장
LIBNAME ex 'C:\Biostat';
RUN;
/*4장 연습문제 불러오기*/
%macro chap04(name=,no=);
%do i=1 %to &no.;
PROC IMPORT DBMS=excel
DATAFILE="C:\Biostat\data_chap04"
OUT=ex.&name.&i. REPLACE;
RANGE="exam4_&i.$";
RUN;
%end;
%mend;
%chap04(name=ex4_,no=4);
EXAMPLE 4.1
PROC IML;
use ex.ex4_1; read all; close ex.ex4_1;
%macro dis(x);
n= nrow(&x);
mean_x=mean(&x);
deviation1=&x-mean(&x);
abs_deviation = abs(deviation1);
deviation2= deviation1`*deviation1;
fq1 = round((nrow(&x)+1)/4);
q1= &x[fq1];
fq3=nrow(&x)+1 -round((nrow(&x)+1)/4);
q3=&x[fq3];
interquartile=q3-q1;
mean_deviation=round(mean(abs_deviation),0.01);
variance= round(sum(deviation2)/(nrow(&x)-1),0.0001);
standarddev=round(sqrt(variance),0.01);
print n mean_x deviation2 interquartile mean_deviation variance standarddev;
%mend;
%dis(x1);%dis(x2);
RUN;
QUIT;
| n | mean_x | deviation2 | interquartile | mean_deviation | variance | standarddev |
|---|---|---|---|---|---|---|
| 7 | 1.8 | 1.12 | 0.8 | 0.34 | 0.1867 | 0.43 |
| n | mean_x | deviation2 | interquartile | mean_deviation | variance | standarddev |
|---|---|---|---|---|---|---|
| 7 | 1.8 | 0.82 | 0.4 | 0.26 | 0.1367 | 0.37 |
EXAMPLE 4.2
PROC IML;
use ex.ex4_2; read all; close ex.ex4_2;
%macro dis2(x);
sum_x=sum(&x);
sum_square=&x`*&x;
mean_x= mean(&x);
ss= sum_square - ((sum_x*sum_x)/nrow(&x));
samplevar_x = round(ss/(nrow(&x)-1), 0.0001);
samplestd_x = round(sqrt(samplevar_x), 0.01);
cv= round(samplestd_x / mean_x,0.01)*100;
print sum_x mean_x samplevar_x samplestd_x cv;
%mend;
%dis2(x1); %dis2(x2);
RUN;
QUIT;
| sum_x | mean_x | samplevar_x | samplestd_x | cv |
|---|---|---|---|---|
| 12.6 | 1.8 | 0.1867 | 0.43 | 24 |
| sum_x | mean_x | samplevar_x | samplestd_x | cv |
|---|---|---|---|---|
| 12.6 | 1.8 | 0.1367 | 0.37 | 21 |
EXAMPLE 4.3
PROC IML;
use ex.ex4_3; read all; close ex.ex4_3;
totsum=repeat(0,5,1);
%macro ind(x);
%do i=1 %to 4 %by 1;
totsum[&i+1] = totsum[&i] + &x[&i]*log10(&x[&i]);
%end;
H = round(((sum(&x)*log10(sum(&x))) - totsum[nrow(sites)+1]) / sum(&x), 0.001);
H_max = round(log10(nrow(sites)), 0.001);
J = round(H/H_max, 0.001);
print H H_max J;
%mend;
%ind(x=sample1);
%ind(x=sample2);
%ind(x=sample3);
RUN;
QUIT;
| H | H_max | J |
|---|---|---|
| 0.602 | 0.602 | 1 |
| H | H_max | J |
|---|---|---|
| 0.255 | 0.602 | 0.424 |
| H | H_max | J |
|---|---|---|
| 0.255 | 0.602 | 0.424 |
EXAMPLE 4.4
DATA ex.ex4_4_1;
SET ex.ex4_4;
IF x3='.' THEN DELETE;
IF code3='.' THEN DELETE;
RUN;
PROC IML;
use ex.ex4_4; read all; close ex.ex4_4;
%macro cod1(x);
sum_x = sum(&x);
sum_sq = sum(&x`*&x);
ss_x = sum_sq - ((sum_x`*sum_x)/nrow(&x));
samplevar_x = round(ss_x/(nrow(&x)-1), 0.01);
samplestd_x = round(sqrt(samplevar_x), 0.01);
mean_x = round(mean(&x), 0.01);
cv = round(samplestd_x/mean_x * 100, 0.01);
print sum_x sum_sq ss_x samplevar_x samplestd_x mean_x cv;
%mend;
%cod1(x1);
%cod1(code1);
RUN;
QUIT;
PROC IML;
use ex.ex4_4_1; read all; close ex.ex4_4_1;
%macro cod2(x);
sum_x = sum(&x);
sum_sq = sum(&x`*&x);
ss_x = sum_sq - ((sum_x`*sum_x)/nrow(&x));
samplevar_x = round(ss_x/(nrow(&x)-1), 0.01);
samplestd_x = round(sqrt(samplevar_x), 0.01);
mean_x = round(mean(&x), 0.01);
cv = round(samplestd_x/mean_x * 100, 0.01);
print sum_x sum_sq ss_x samplevar_x samplestd_x mean_x cv;
%mend;
%cod2(x3);
%cod2(code3);
RUN;
QUIT;
| sum_x | sum_sq | ss_x | samplevar_x | samplestd_x | mean_x | cv |
|---|---|---|---|---|---|---|
| 6765 | 5720695 | 41.875 | 5.98 | 2.45 | 845.63 | 0.29 |
| sum_x | sum_sq | ss_x | samplevar_x | samplestd_x | mean_x | cv |
|---|---|---|---|---|---|---|
| 45 | 295 | 41.875 | 5.98 | 2.45 | 5.63 | 43.52 |
| sum_x | sum_sq | ss_x | samplevar_x | samplestd_x | mean_x | cv |
|---|---|---|---|---|---|---|
| 6300 | 6815000 | 200000 | 40000 | 200 | 1050 | 19.05 |
| sum_x | sum_sq | ss_x | samplevar_x | samplestd_x | mean_x | cv |
|---|---|---|---|---|---|---|
| 63 | 681.5 | 20 | 4 | 2 | 10.5 | 19.05 |
교재: Biostatistical Analysis (5th Edition) by Jerrold H. Zar
**이 글은 22학년도 1학기 의학통계방법론 과제 자료들을 정리한 글 입니다.**
