[의학통계방법론] Ch3. Measures of Central Tendency

10 Mar 2022 in Study log / Study / 의학통계방법론 on R, Sas, Blog, Jekyll, Jupyter, Data, Python

Measures of Central Tendency
R 프로그램 결과
- 3장
SAS 프로그램 결과
- 3장

Measures of Central Tendency

예제 데이터파일 다운로드

정리내용 접기/펼치기 버튼

3.1 The Arithmetic Mean

산술평균 (arithmetic mean)
- 모든 관측값들의 합을 표본크기로 나눈 것
- 데이터는 구간 척도(interval scale), 비 척도(ratio scale)이어야 한다.
- 모든 값들이 계산에 이용된다.
- 유일하다.(unique)
- 평균으로부터의 편차의 합은 항상 0 이다.
- 이상치에 영향을 받는다.

\[\overline X= \frac {\sum_{i=1}^{n}X_i} {n}\]

가중평균 (weighted arithmetic mean)
- 서로 다른 표본크기를 가지는 표본들의 평균값을 구할 때 사용

\[\overline X_w= \frac {\sum_{i=1}^{n}w_i \cdot X_i} {\sum_{i=1}^{n}w_i}\]

3.2 The Median

중위수 / 중앙값 (median)
- 정렬된 자료에서 가장 가운데 위치한 수
- 이상치에 영향을 받지 않는다.
- 유일하다.(unique)
- 예) 1,2,6,7,8 (n=5, 홀수): 3번째 값 = 6.
- 예) 1,2,7,8,9,10 (n=6, 짝수): 3번째와 4번째 값의 평균 = 7.5
- 실제 예) 소득, 병원 입원기간 (데이터가 중앙에 몰려있는 자료)
도수분포표에서의 중위수 계산
- 누적 도수를 이용하여 중위수가 있을 구간을 찾는다.
- 구간 크기 (interval size)를 계산한다.
- 총 빈도(n)을 계산한다.
- 예상 구간 바로 전 구간까지의 누적빈도를 계산한다.

\[\begin{aligned} median = Lower\space \space limit \space of \space Interval + \frac{0.5n-Cummulative \space Frequency}{Num. of \space observations \space in \space interval} \cdot Interval \space size \end{aligned}\]

중심경향 (central tendency)의 측도는
- 이상치가 없다면 일반적으로 평균 사용
- 이상치가 있는 경우에는 이에 덜 민감한 중위수 사용

3.3 The Mode

최빈값 (mode)
- 가장 빈번하게 관측된 측정값
- 이상치에 영향을 받지 않는다.
- 수치형 자료나 범주형 자료 모두에 사용될 수 있다.
- 최빈값이 없을 수도 있다.
- 여러개의 최빈값이 존재할 수도 있다. (not unique)

3.4 Other Measures of Central Tendency

기하평균 (geometric mean; GM)
- 데이터가 양수이면서 오른쪽으로 치우친 경우 사용 (0 포함된 데이터 경우 사용 X)
- 데이터가 변화의 비(ratio of change)로 측정된 경우
- 두 그룹에 대하여 데이터의 범위(range)가 다른 경우
- 예: 인구 증가율
- 데이터가 같지 않다면 기하평균은 산술평균보다 항상 작다.

\[\overline X_G =^n \sqrt{X_1 X_2 X_3 \cdots X_n}\]

기하평균의 필요성
- 곱셈으로 계산하는 값에서의 평균을 계산하고자 할 때 기하 평균을 사용한다.
- 예를 들어 어떤 값이 처음에 1000이고, 첫 해에 10% 증가하고，그 다음 해 에 20% 증가하고, 그 다음 해에 15% 감소했다고 할 때 결과 값은 처음의 값 1000에 1.1，1.2, 0.85의 기하평균을 세 번 곱한 값이 된다. 1.1，1.2, 0.85 의 기하평균 (1.1 x 1.2 x 0.85)/3 = 1.0391… 이므로，3년동안 평균 3.91%씩 증가한 셈이다. 즉，1000 x 1.1 x 1.2 x 0.85 = 1000(1.0391)3이다.
조화평균 (harmonic mean; HM)
- 데이터가 양수이며 비척도(ratio scale)인 경우 사용
- 평균적인 변화율을 구할 때 주로 사용
- 데이터가 양수이고 같지 않다면 조화평균<기하평균<산술평균 이다.

\[\overline X_H = \frac{n}{\sum \frac{1}{X_i}}\]

조화평균의 필요성
- 평균적인 변화율을 구하고자 할 때 사용
- 예를 들어, 전체 거리의 절반을 40km/h의 속도로 달리고, 남은 절반을 60km/h 로 달렸다면，평균 속력은 40과 60의 조화 평균인 48km/h가 된다.
절단평균 (truncated mean, trimmed mean)
- 데이터의 양쪽 꼬리부분 즉, 작은 값이나 큰 값의 일부를 제외하고 구한 평균
- 보통 5% ~ 25%의 자료를 버리고 구한다.
- 특이치가 있는 경우 덜 민감한 평균을 계산할 수 있다.
- 분포가 대칭적이지 않을 경우에는 편향된 평균값을 계산할 수 있게 된다.
사분위평균 (interquartile mean; IQM)
- 데이터의 상위 25%, 하위 25%를 버리고 구한 평균

\[\overline X= \frac{2}{n}{\sum_{i=(\frac{n}{4})+1}^{\frac{3n}{4}} X_i}\]

R 프로그램 결과

R 접기/펼치기 버튼

패키지

설치된 패키지 접기/펼치기 버튼

getwd()

## [1] "C:/Biostat"

library("readxl")
library("ggplot2")
library("Hmisc")
library("psych")

엑셀파일불러오기

library('readxl')
#모든 시트를 하나의 리스트로 불러오는 함수
read_excel_allsheets <- function(file, tibble = FALSE) {
  sheets <- readxl::excel_sheets(file)
  x <- lapply(sheets, function(X) readxl::read_excel(file, sheet = X))
  if(!tibble) x <- lapply(x, as.data.frame)
  names(x) <- sheets
  x
}

3장

3장 연습문제 불러오기

#data_chap03에 연습문제 3장 모든 문제 저장
data_chap03 <- read_excel_allsheets("data_chap03.xls")

#연습문제 각각 데이터 생성
for (x in 1:length(data_chap03)){
  assign(paste0('ex3_',1:length(data_chap03))[x],data_chap03[x])
  }

#연습문제 데이터 형식을 리스트에서 데이터프레임으로 변환
for (x in 1:length(data_chap03)){
  assign(paste0('ex3_',1:length(data_chap03))[x],data.frame(data_chap03[x]))
  }

EXAMPLE 3.1

#데이터셋
ex3_1

##    Length
## 1     3.3
## 2     3.5
## 3     3.6
## 4     3.6
## 5     3.7
## 6     3.8
## 7     3.8
## 8     3.8
## 9     3.9
## 10    3.9
## 11    3.9
## 12    4.0
## 13    4.0
## 14    4.0
## 15    4.0
## 16    4.1
## 17    4.1
## 18    4.1
## 19    4.2
## 20    4.2
## 21    4.3
## 22    4.3
## 23    4.4
## 24    4.5

sum_x <- sum(ex3_1$Length) ; cat('Sum of X =', sum_x)

## Sum of X = 95

n <- length(ex3_1$Length); cat('Sample Size =', n)

## Sample Size = 24

x_bar <- mean(ex3_1$Length); cat('Mean of X =', x_bar)

## Mean of X = 3.958333

\[\begin{aligned} \sum X_i &= 95.0 \ cm \\ n &= 24 \\ \bar{X} &= \frac{\sum X_i}{n} = \frac{95.0\ cm}{24} = 3.96\ cm \end{aligned}\] 나비의 날개 길이를 측정하기 위해 추출된 24마리의 나비들을 관측한 결과,
날개의 합은 95 cm 이며 평균은 3.96 cm 이다.

EXAMPLE 3.2

#데이터셋
ex3_2

##    exam3_2.X exam3_2.Freq
## 1        3.3            1
## 2        3.4            0
## 3        3.5            1
## 4        3.6            2
## 5        3.7            1
## 6        3.8            3
## 7        3.9            3
## 8        4.0            4
## 9        4.1            3
## 10       4.2            2
## 11       4.3            2
## 12       4.4            1
## 13       4.5            1

가중평균 계산

library(Hmisc) # wtd.mean 사용하기 위해
xi <- ex3_2$exam3_2.X
fi <- ex3_2$exam3_2.Freq
wm <- wtd.mean(xi, weights=fi) #가중평균
round(wm,2)

## [1] 3.96

도수분포표에서 가중평균을 구할 때에는 각 표본에 가중을 두어 합을 구한 후 가중치의 합을 나눈다.

sum_fixi <- sum(fi*xi) # 가중합
sum_fi <- sum(fi) #가중치 합
w_mean<-sum_fixi/sum_fi #가중평균
cat("가중합 = ",sum_fixi,"   ","가중치 합 = ",sum_fi,"   ","가중평균 = ",w_mean)

## 가중합 =  95     가중치 합 =  24     가중평균 =  3.958333

\[\begin{aligned} \overline X_w &= \frac {\sum_{i=1}^{n}f_i \cdot X_i} {\sum_{i=1}^{n}f_i} = \frac{95.0 cm}{24} = 3.96 \end{aligned}\]

중위수 계산
중위수는 정렬된 자료에서 중앙에 위치한 수이다.
도수분포표에서는 R에 내장되어 있는 함수인 wtd.quantile() 함수를 사용해서 중위수를 구할 수 있다.

x.median <- wtd.quantile(xi, weights=fi, probs=c(0,.25,.5,.75,1), type=c("i/n"))
wmed <- round(x.median,5)
wvar <- wtd.var(xi, weights=fi) # 분산
cat("wtd.quatile() 로 구한 중위수","\n","중위수 = ",wmed[3],"   분산 = ",wvar)

## wtd.quatile() 로 구한 중위수 
##  중위수 =  3.925    분산 =  0.08514493

도수분포표에서 중위수를 구하기 위해서는 다음의 식을 이용하여 구한다. \[\begin{aligned} median = Lower\space \space limit \space of \space Interval + \frac{0.5n-Cummulative \space Frequency}{Num. of \space observations \space in \space interval} \cdot Interval \space size \end{aligned}\] 해당 데이터를 표로 작성하면 다음과 같다.

\(X_i(cm)\)	\(f_i\)	\(f_iX_i(cm)\)
3.3	1	3.3
3.4	0	0
3.5	1	3.5
3.6	2	7.2
3.7	1	3.7
3.8	3	11.4
3.9	3	11.7
4.0	4	16.0
4.1	3	12.3
4.2	2	8.4
4.3	2	8.6
4.4	1	4.4
4.5	1	4.5
Sum	24	95

1) 예상 구간의 하한값
24개의 관측치 중 11개의 관측치는 4.0cm 보다 작고 9개는 크다.
그러므로 통상적인 중위수는 12번째 값이 포함된 4.0 이라 하기는 어렵다.
하지만 중위수는 [3.95,4.05] 이내에 있을 필요가 있다고 생각해야한다.
따라서 예상구간의 하한값은 3.95 가 된다.

2) 총 빈도

sum(fi)

## [1] 24

3) 누적 빈도
누적빈도는 4.0이 오기 전 까지의 누적 빈도를 사용한다.

which(fi==4.0) # 8번째 인덱스에 4.0 위치

## [1] 8

cf <- cumsum(fi)
cf[7] #7번째 인덱스 까지의 누적빈도

## [1] 11

4) 구간 크기

diff(xi) #0.1

##  [1] 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1

이렇게 구한 값들로 중위수를 구하면 다음과 같다.
\[\begin{aligned} median =3.95\space cm + \frac{0.5\cdot24-11}{4} \cdot 0.1=3.95 \space cm+0.025 \space cm=3.975\space cm \end{aligned}\] 수식을 이용한 도수분포표에서의 중위수는 3.975로 나왔다.

library('ggplot2')
ggplot(ex3_1, aes(x=Length)) +  geom_histogram(binwidth = 0.1, fill='#8dd3c7',colour='#ffffb3')+
  scale_x_continuous(breaks = seq(0,4.5,0.1))

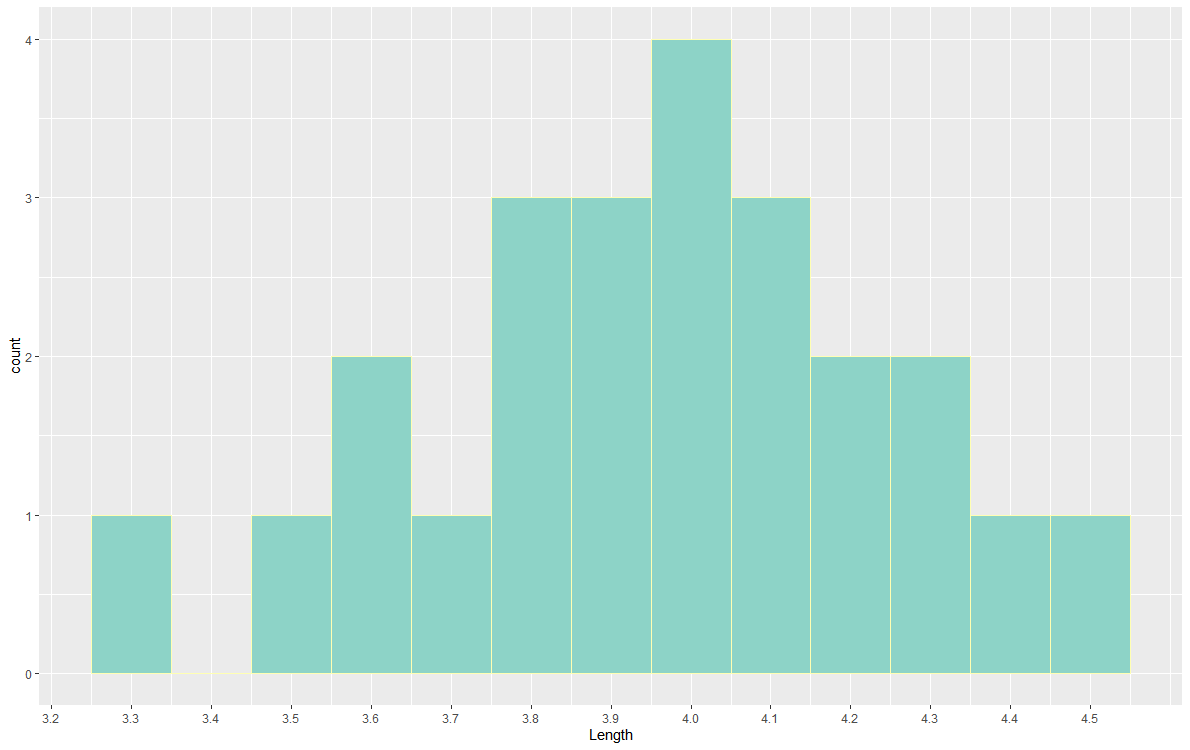
히스토그램
- 히스토그램을 보면 날개의 길이가 4인 경우의 빈도수가 4로 가장 많은것을 알 수 있다.
- 나비 날개 길이의 frequency table 출력 결과를 살펴보면
  표본평균 값이 3.96이고 중앙값이 3.975이므로 두 값이 서로 비슷한 것을 확인할 수 있다.
  따라서 거의 치우치지 않은 분포의 형태를 띄고 있는 것을 알 수 있고 히스토그램을 통해서도 확인할 수 있다.

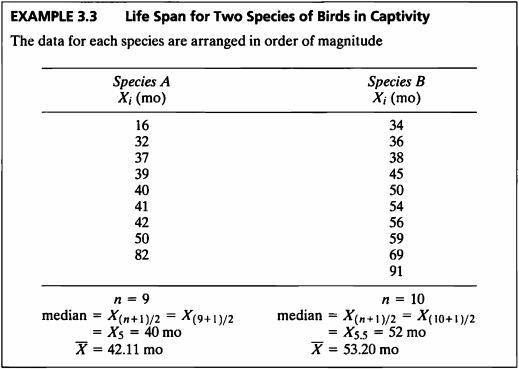
EXAMPLE 3.3

#데이터셋
ex3_3

##    exam3_3.Group exam3_3.LifeSpan
## 1              A               16
## 2              A               32
## 3              A               37
## 4              A               39
## 5              A               40
## 6              A               41
## 7              A               42
## 8              A               50
## 9              A               82
## 10             B               34
## 11             B               36
## 12             B               38
## 13             B               45
## 14             B               50
## 15             B               54
## 16             B               56
## 17             B               59
## 18             B               69
## 19             B               91

ex3_3$exam3_3.LifeSpan

##  [1] 16 32 37 39 40 41 42 50 82 34 36 38 45 50 54 56 59 69 91

ex3_3_a <- subset(ex3_3,exam3_3.Group=="A")
ex3_3_b <- subset(ex3_3,exam3_3.Group=="B")
a_n <- length(ex3_3_a$exam3_3.Group) 
b_n <- length(ex3_3_b$exam3_3.Group)
a_med <- median(ex3_3_a$exam3_3.LifeSpan) 
b_med <- median(ex3_3_b$exam3_3.LifeSpan)
a_mn <- round(mean(ex3_3_a$exam3_3.LifeSpan),2) ;
b_mn <- mean(ex3_3_b$exam3_3.LifeSpan)

cat(" Number of Species A = ",a_n,",  Median of Species A = ",a_med, ",  Mean of Species A = ",a_mn,"\n",
    "Number of Species B = ",b_n,",  Median of Species B = ",b_med, ",  Mean of Species B = ",b_mn)

##  Number of Species A =  9 ,  Median of Species A =  40 ,  Mean of Species A =  42.11 
##  Number of Species B =  10 ,  Median of Species B =  52 ,  Mean of Species B =  53.2

	Species A	Species B
\(n\)	9	10
\(median\)	40	52
\(\overline X\)	42.11	53.20

A종의 새 9마리와 B종의 새 10마리를 관측했을 때, A종의 경우 수명 중위수는 40개월, 평균 수명은 42.11개월이며 B종의 경우 수명 중위수는 52개월, 평균 수명은 53.20개월로 측정되었다.

EXAMPLE 3.4

#데이터셋
ex3_4

##   exam3_4.decade exam3_4.population exam3_4.ratio
## 1              0              10000            NA
## 2              1              10500          1.05
## 3              2              11550          1.10
## 4              3              13860          1.20
## 5              4              18156          1.31

기하평균은 인구증가율 등을 구할 때 사용되는 평균이며 데이터가 같지 않다면 기하평균은 산술평균보다 항상 작다는 특징이 있다. \[\overline X_G = \begin{cases} Method \ 1) ^n \sqrt{X_1 X_2 X_3 \cdots X_n} \\ Method \ 2) antilog(\frac{logX_1 + logX_2 + \cdots + logX_n}{n}) \\ \end{cases}\]

Manually

x_bar <- mean(na.omit(ex3_4$exam3_4.ratio))
geo_mean_x_method1 <- exp(mean(log(na.omit(ex3_4$exam3_4.ratio)))) 
geo_mean_x_method2 <- prod(na.omit(ex3_4$exam3_4.ratio)) ^ (1/length(na.omit(ex3_4$exam3_4.ratio)))
cat('Geometric Mean Manually =', '('  ,'method1 =', geo_mean_x_method1, ',' ,'method2 =' ,geo_mean_x_method2,')')

## Geometric Mean Manually = ( method1 = 1.160803 , method2 = 1.160803 )

Package

library(psych)
geo_mean_x_package <- geometric.mean(ex3_4$exam3_4.ratio) ; cat('Geometric Mean with psych package =', geo_mean_x_package)

## Geometric Mean with psych package = 1.160803

기하 평균은 데이터 곱의 n 제곱근(Method 1)으로 나타낼 수 있으며,
데이터 로그 변환의 산술 평균을 다시 역로그변환(지수변환) (Method 2)으로 나타낼 수 있다.
변화율의 산술 평균은 1.165이며, 이 때 기하 평균은 두 가지 방법 및 패키지를 이용하였을 때 1.1608로 동일하게 산출된다.

first_p <- ex3_4$exam3_4.population[1] # 초기 population
final_p_a  <- round(first_p*mean(ex3_4$exam3_4.ratio[2:5])^4)
final_p_g <- round(first_p*round(geometric.mean(ex3_4$exam3_4.ratio[2:5]),4)^4)
cat(" 산술평균으로 구한 Final Population = ",final_p_a,"\n","기하평균으로 구한 Final Population = ",final_p_g) 

##  산술평균으로 구한 Final Population =  18421 
##  기하평균으로 구한 Final Population =  18156

앞서 구한 산술평균과 기하평균을 이용해 마지막 인구집단 사이즈를 구해보았다.

EXAMPLE 3.5

#데이터셋
ex3_5

##    X
## 1 40
## 2 20

조화평균은 평균의 변화율을 구할 떄 주로 사용되며 데이터가 양수이고 비척도인 경우에 이용한다 \[\overline X_H = \frac{n}{\sum \frac{1}{X_i}}\]

Manually

harmonic_mean_manual <- round(length(ex3_5$X) / sum(1/ex3_5$X),2) ; cat('Harmonic Mean Manually =', harmonic_mean_manual)

## Harmonic Mean Manually = 26.67

Package

library(psych)
harmonic_mean_package <- round(harmonic.mean(ex3_5$X),2) ; cat('Harmonic Mean with psych package =', harmonic_mean_package)

## Harmonic Mean with psych package = 26.67

수식을 이용한 방식과 패키지를 이용하여 조화 평균을 산출 했을 때 값이 26.67로 같은 값이 산출된다.

xm <- mean(ex3_5$X)
cat("산술평균=", xm, "km/h,   조화평균=",harmonic_mean_manual,"km/h")

## 산술평균= 30 km/h,   조화평균= 26.67 km/h

이처럼 전체 거리를 절반은40km/h로 달리고 나머지는 20km/h로 달렸다면,
평균속력은 40과 20의 조화평균인 26.67 km/h가 된다.

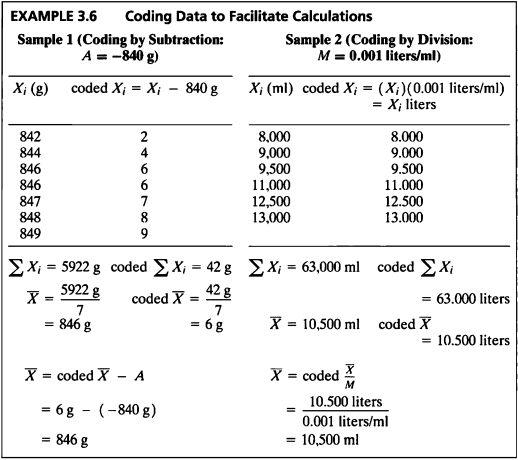
EXAMPLE 3.6

#데이터셋
ex3_6

##   exam3_6.X1 exam3_6.code1 exam3_6.X2 exam3_6.code2
## 1        842             2       8000          8000
## 2        844             4       9000          9000
## 3        846             6      95000         95000
## 4        846             6      11000         11000
## 5        847             7      12500         12500
## 6        848             8      13000         13000
## 7        849             9         NA            NA

The mean of the coded values is equal to \(\overline X - 840 g\).

A <- -840 ; M <- 0.001

sum_sample1 <- sum(ex3_6$exam3_6.X1)
coded_sum_sample1 <- sum(ex3_6$exam3_6.code1)
mean_sample1 <- mean(ex3_6$exam3_6.X1)
coded_mean_sample1 <- mean(ex3_6$exam3_6.code1)

mean_sample1 <-  coded_mean_sample1-A
mean_sample1

## [1] 846

The mean of the coded values is equal to \(\overline X * M\).

#데이터 오기 수정하기
ex3_6$exam3_6.X2[3] <- ex3_6$exam3_6.X2[3]/10
ex3_6$exam3_6.code2[3] <- ex3_6$exam3_6.code2[3]/10

#결측값제외하고 계산
sum_sample2 <- sum(na.omit(ex3_6$exam3_6.X2))
coded_sum_sample2 <- sum(na.omit(ex3_6$exam3_6.code2*M))
mean_sample2 <- mean(na.omit(ex3_6$exam3_6.X2))
coded_mean_sample2 <- mean(na.omit(ex3_6$exam3_6.code2*M))

mean_sample2 <-  coded_mean_sample2 / M
mean_sample2

## [1] 10500

stat / Group	Sample 1	Sample 2
Sum	5922	63000
coded Sum	42	63
Mean	846	10500
coded Mean	6	10.5

SAS 프로그램 결과

sas 접기/펼치기 버튼

3장

LIBNAME ex 'C:\Biostat';
RUN;

/*3장 연습문제 불러오기*/
%macro chap03(name=,no=);
%do i=1 %to &no.;
	PROC IMPORT DBMS=excel
		DATAFILE="C:\Biostat\data_chap03"
		OUT=ex.&name.&i. REPLACE;
		RANGE="exam3_&i.$";
	RUN;
%end;
%mend;

%chap03(name=ex3_,no=6);